题目内容
20.在极坐标中,直线l的方程为ρ(3cosθ-4sinθ)=2,曲线C的方程为ρ=m(m>0).(1)求直线l与极轴的交点到极点的距离;
(2)若曲线C上恰好存在两个点到直线l的距离为$\frac{1}{5}$,求实数m的取值范围.
分析 (1)令θ=0,得ρ(3cos0-4sin0)=2,由此能求出直线l与极轴的交点到极点的距离.
(2)先求出直线l和曲线C的直角坐标方程,由曲线C表示以原点为圆心,以m为半径的圆,且原点到直线l的距离为$\frac{2}{5}$,结合题设条件能求出实数m的取值范围.
解答 解:(1)∵直线l的方程为ρ(3cosθ-4sinθ)=2,
∴令θ=0,得ρ(3cos0-4sin0)=2,
∴3ρ=2,
∴直线l与极轴的交点到极点的距离ρ=$\frac{2}{3}$.
(2)直线l的直角坐标方程为3x-4y-2=0,曲线C的直角坐标方程为x2+y2=m2,
曲线C表示以原点为圆心,以m为半径的圆,且原点到直线l的距离为$\frac{2}{5}$,
∵曲线C上恰好存在两个点到直线l的距离为$\frac{1}{5}$,
∴$\frac{1}{5}<m<\frac{3}{5}$.
∴实数m的取值范围是($\frac{1}{5}$,$\frac{3}{5}$).
点评 本题考查直线与极轴的交点到极点的距离的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
10.设$α,β∈(0,\frac{π}{2})$且$tanα-tanβ=\frac{1}{cosβ}$,则( )
| A. | $3α+β=\frac{π}{2}$ | B. | $2α+β=\frac{π}{2}$ | C. | $3α-β=\frac{π}{2}$ | D. | $2α-β=\frac{π}{2}$ |
8.从3个英语教师和5个语文教师中选取4名教师参加外事活动,其中至少要有一名英语教师,则不同的选法共有( )
| A. | $A_3^1A_5^3+A_3^2A_5^2+A_3^3A_5^1$ | |
| B. | $C_3^1C_5^3+C_3^2C_5^2+C_3^3C_5^1$ | |
| C. | $C_3^1C_7^3$ | |
| D. | $({C_3^1C_5^3+C_3^2C_5^2+C_3^3C_5^1})A_4^4$ |
9.在△ABC中,角A,B,C的对边分别是a,b,c,面积为S,若S≥$\frac{1}{2}$ab,b2+ac=a2+c2,则a:b:c等于( )
| A. | 3:4:5 | B. | 1:1:$\sqrt{2}$ | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | 1:$\sqrt{3}$:2 |
10.函数y=lnx+x在点(1,1)处的切线方程是( )
| A. | 2x-y-1=0 | B. | 2x+y-1=0 | C. | x-2y+1=0 | D. | x+2y-1=0 |
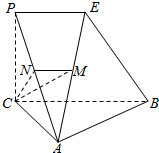 如图,在四棱锥A-BCPE中,侧面PAC为正三角形,∠ACB=90°,二面角P-AC-B为直二面角,PE∥BC且$\frac{PE}{CB}$=μ(μ>0),点M,N分别是侧棱AE、AP上的点,且$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ(0<λ<1)
如图,在四棱锥A-BCPE中,侧面PAC为正三角形,∠ACB=90°,二面角P-AC-B为直二面角,PE∥BC且$\frac{PE}{CB}$=μ(μ>0),点M,N分别是侧棱AE、AP上的点,且$\frac{AM}{AE}$=$\frac{AN}{AP}$=λ(0<λ<1)