题目内容
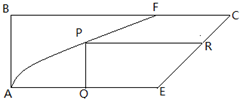 如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,
如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,公园形状为直角梯形QPRE(其中线段EQ和RP为两条底边).记QP=x(km),公园面积为S(km2).
(Ⅰ)以A为坐标原点,AE所在直线为x轴建立平面直角坐标系,求AF所在抛物线的标准方程;
(Ⅱ)求面积S(km2)关于x(km)的函数解析式;
(Ⅲ)求面积S(km2)的最大值.
分析:(Ⅰ)设抛物线y2=2px,根据点F(4,2)在抛物线上,可求AF所在抛物线的标准方程;
(Ⅱ)公园形状为直角梯形QPRE,所以利用面积公式可求,应注意x的取值范围;
(Ⅲ)先求导函数,令导数为0,得x=
,利用函数在(0,2)上是单峰函数,可求函数的最值.
(Ⅱ)公园形状为直角梯形QPRE,所以利用面积公式可求,应注意x的取值范围;
(Ⅲ)先求导函数,令导数为0,得x=
| 4 |
| 3 |
解答: 解:(Ⅰ)设抛物线y2=2px
解:(Ⅰ)设抛物线y2=2px
∵点F(4,2)在抛物线上,∴22=2p×4,∴2p=1,∴y2=x
(Ⅱ)设P(x2,x) 则QE=AE-AQ=4-x2
∵∠PRE=∠C=45°∴PR=QE+x=4-x2+xS=
(4-x2+4-x2+x)=-x3+
x2+4x(0<x<2)
(Ⅲ)S'(x)=-3x2+x+4令S'(x)=0则x=-1(舍去)或x=
当0<x<
时,S'>0,∴S(x)递增;当
<x<2时,S'<0,∴S(x)递减;
∴当x=
km时,Smax=
km2
 解:(Ⅰ)设抛物线y2=2px
解:(Ⅰ)设抛物线y2=2px∵点F(4,2)在抛物线上,∴22=2p×4,∴2p=1,∴y2=x
(Ⅱ)设P(x2,x) 则QE=AE-AQ=4-x2
∵∠PRE=∠C=45°∴PR=QE+x=4-x2+xS=
| x |
| 2 |
| 1 |
| 2 |
(Ⅲ)S'(x)=-3x2+x+4令S'(x)=0则x=-1(舍去)或x=
| 4 |
| 3 |
当0<x<
| 4 |
| 3 |
| 4 |
| 3 |
∴当x=
| 4 |
| 3 |
| 104 |
| 27 |
点评:本题注意考查函数模型的建立,考查利用导数解决函数的最值问题,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.
如图,在矩形地块ABCD中有两条道路AF,EC,其中AF是以A为顶点的抛物线段,EC是线段.AB=2km,BC=6km,AE=BF=4km.在两条道路之间计划修建一个花圃,花圃形状为直角梯形QPRE(线段EQ和RP为两个底边,如图所示).求该花圃的最大面积.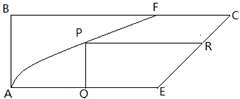 如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,
如图,直角梯形地块ABCE,AF、EC是两条道路,其中AF是以A为顶点、AE所在直线为对称轴的抛物线的一部分,EC是线段.AB=2km,BC=6km,AE=BF=4km.计划在两条道路之间修建一个公园,