题目内容
在平面直角坐标系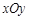 中,直线
中,直线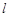 的参数方程是
的参数方程是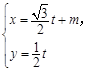 (t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线
(t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线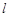 与圆C相切,求实数m的值.
与圆C相切,求实数m的值.
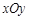 中,直线
中,直线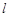 的参数方程是
的参数方程是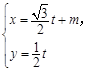 (t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线
(t是参数), 以原点为极点,x轴的正半轴为极轴建立极坐标系,若圆C的极坐标方程是ρ=4cosθ,且直线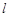 与圆C相切,求实数m的值.
与圆C相切,求实数m的值.6或 .
.
 .
.试题分析:把直线
 的参数方程消去参数
的参数方程消去参数 可得普通方程为
可得普通方程为 ,把圆的极坐标方程
,把圆的极坐标方程 化为直角坐标方程为
化为直角坐标方程为 ,即
,即 ,利用圆心到直线的距离等于圆的半径可得
,利用圆心到直线的距离等于圆的半径可得 的值.
的值.由
 ,得
,得 ,所以
,所以 ,即圆
,即圆 的方程为
的方程为 ,
, 又由
 消
消 ,得
,得 ,由直线
,由直线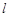 与圆
与圆 相切,
相切,所以
 ,即
,即 或
或 10分
10分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
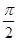 ).若直线l过点P,且倾斜角为
).若直线l过点P,且倾斜角为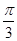 ,圆C以M为圆心, 4为半径.
,圆C以M为圆心, 4为半径.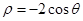 的圆心的极坐标为( )
的圆心的极坐标为( )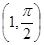


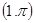
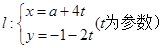 ,圆
,圆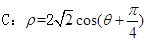 (极轴与x轴非负半轴重合,且单位长度相同),若直线l被圆C截得的弦长为
(极轴与x轴非负半轴重合,且单位长度相同),若直线l被圆C截得的弦长为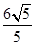 ,则实数a的值为 .
,则实数a的值为 .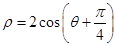 ,则该圆的半径是 .
,则该圆的半径是 .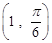 为圆心,1为半径的圆的极坐标方程是 .
为圆心,1为半径的圆的极坐标方程是 .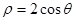 关于直线
关于直线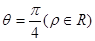 对称的圆的的极坐标方程是 .
对称的圆的的极坐标方程是 .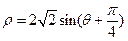 所表示的曲线的直角坐标方程是 。
所表示的曲线的直角坐标方程是 。