题目内容
16.将函数y=f(x)的图象上每一点的纵坐标缩小为原来的$\frac{1}{2}$倍,再将横坐标压缩为原来的$\frac{1}{2}$倍,再将整个图象沿x轴向左平移$\frac{π}{3}$,可得y=sinx,则原来的函数f(x)=2sin($\frac{1}{2}$x-$\frac{π}{3}$).分析 利用逆向思维,将y=sinx沿x轴向右平移$\frac{π}{3}$,再将横坐标伸长为原来的2倍,最后纵坐标伸长为原来的2倍,可得答案.
解答 解:将y=sinx沿x轴向右平移$\frac{π}{3}$,得到y=sin(x-$\frac{π}{3}$)的图象,再将横坐标伸长为原来的2倍,得到y=sin($\frac{1}{2}$x-$\frac{π}{3}$)的图象,最后纵坐标伸长为原来的2倍,所求函数解析式为:f(x)=2sin($\frac{1}{2}$x-$\frac{π}{3}$).
故答案为:2sin($\frac{1}{2}$x-$\frac{π}{3}$).
点评 本题考查函数y=Asin(ωx+φ)的图象变换,考查逻辑思维能力,逆向思维的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若tan(α+45°)<0,则下列结论正确的是( )
| A. | sinx<0 | B. | cosx<0 | C. | sin2x<0 | D. | cos2x<0 |
8.若f(x+$\frac{1}{x}$)=x2+$\frac{1}{{x}^{2}}$+1,则函数f(x)的解析式为( )
| A. | f(x)=x2-1 | B. | f(x)=x2-1(x≥2) | ||
| C. | f(x)=x2-1(x≤-2) | D. | f(x)=x2-1(x≥2或x≤-2) |
12. 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )
 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥A1C1,B1C⊥AC1,AB=2,AC=1,则该三棱柱的体积为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
 如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.
如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,BF⊥AE,F是垂足.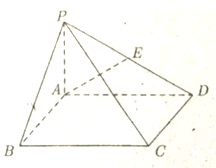 在四棱锥P-ABCD中,PA⊥底面ABCD,PA=1,底面ABCD是正方形,E是PD的中点,PD与底面ABCD所成的角为$\frac{π}{6}$,求异面直线AE与PC 所成的角的大小.
在四棱锥P-ABCD中,PA⊥底面ABCD,PA=1,底面ABCD是正方形,E是PD的中点,PD与底面ABCD所成的角为$\frac{π}{6}$,求异面直线AE与PC 所成的角的大小.