题目内容
定义在区间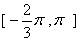 上的函数
上的函数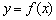 的图象关于直线
的图象关于直线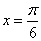 对称,当
对称,当
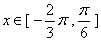 时函数
时函数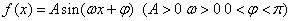 图象如图所示.
图象如图所示.
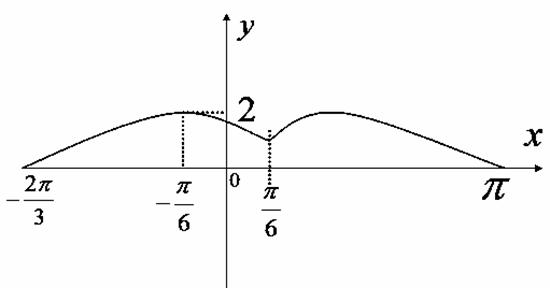
(Ⅰ)求函数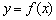 在
在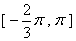 的表达式;(Ⅱ)求方程
的表达式;(Ⅱ)求方程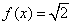 的解;
的解;
(Ⅲ)是否存在常数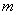 的值,使得
的值,使得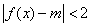 在
在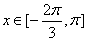 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅰ)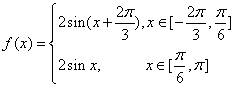 ;(Ⅱ)
;(Ⅱ)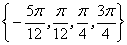 ;(Ⅲ)
;(Ⅲ)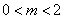
【解析】
试题分析:(Ⅰ)由函数的图像可分两段求解:当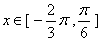 ,
,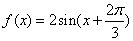 ;当
;当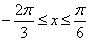 ,
, .注意运用图像的对称性.故
.注意运用图像的对称性.故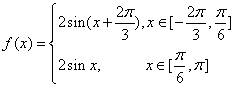 ;(Ⅱ)结合(Ⅰ)中的解
;(Ⅱ)结合(Ⅰ)中的解 (Ⅱ)当
(Ⅱ)当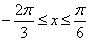 时,
时,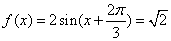
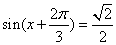
∴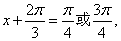 即
即
当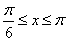 时,
时,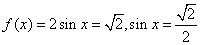 ∴
∴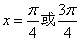
∴方程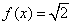 的解集是
的解集是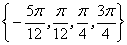 ………………8分
………………8分
(Ⅲ)存在. 假设存在,由条件得: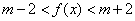 在
在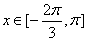 上恒成立
上恒成立
即 ,由图象可得:
,由图象可得: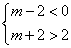 ∴
∴ 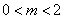 ………………12分
………………12分
考点:1.利用函数图像求函数解析式;2.解三角方程;3.利用函数图像处理函数不等式的恒成立问题

练习册系列答案
相关题目
 的导数为
的导数为 ,且
,且 ,则
,则 的值是
的值是  ,则满足方程
,则满足方程 的所有的
的所有的 的值为 .
的值为 .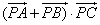 的最小值是( )
的最小值是( ) B.
B. 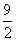 C.2 D.-2
C.2 D.-2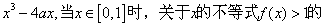 解集为空集,则满足条件的实数a的取值范围是 .
解集为空集,则满足条件的实数a的取值范围是 .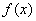 的导函数
的导函数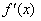 的图象如图所示,那么函数
的图象如图所示,那么函数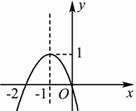
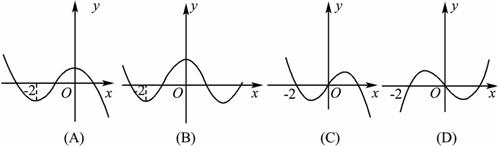
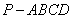 中,底面
中,底面 是平行四边形,
是平行四边形,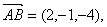
 则直线
则直线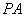 与底面
与底面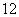 B.
B.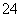 C.
C.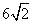 D.
D.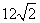
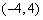 的抛物线的标准方程是 .
的抛物线的标准方程是 .