题目内容
已知
=
,
=
,
=
,
=
,
=
,设t∈R,如果3
=
,2
=
,
=t(
+
),那么t为何值时,C,D,E 三点在一条直线上?
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OD |
| d |
| OE |
| e |
| a |
| c |
| b |
| d |
| e |
| a |
| b |
分析:C,D,E 三点在一条直线上的充要条件是存在实数k,使
=k
,代入已知可得(t-3+3k)
=(2k-t)
,分
,
共线,和
,
不共线,两种情形来考虑,可得答案.
| CE |
| CD |
| a |
| b |
| a |
| b |
| a |
| b |
解答:解:由题意可得
=
-
=2
-3
,
=
-
=(t-3)
+t
,
C,D,E 三点在一条直线上的充要条件是存在实数k,使
=k
,
即(t-3)
+t
=-3k
+2k
,整理得(t-3+3k)
=(2k-t)
,
若
,
共线,则t可为任意实数,
若
,
不共线,则有
,解得t=
,
综上可知:
,
共线,则t可为任意实数,当
,
不共线时,t=
| CD |
| d |
| c |
| b |
| a |
| CE |
| e |
| c |
| a |
| b |
C,D,E 三点在一条直线上的充要条件是存在实数k,使
| CE |
| CD |
即(t-3)
| a |
| b |
| a |
| b |
| a |
| b |
若
| a |
| b |
若
| a |
| b |
|
| 6 |
| 5 |
综上可知:
| a |
| b |
| a |
| b |
| 6 |
| 5 |
点评:本题考查向量的共线定理,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目
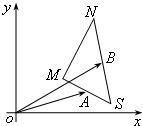 如图,已知
如图,已知