题目内容
已知| OA |
| a |
| OB |
| b |
| a |
| b |
| a |
| b |
(1)当△AOB的面积最大时,求
| a |
| b |
(2)在(1)的条件下,判断△AOB的形状,并说明理由.
分析:(1)由面积公式得,S△AOB=
|
•|
|sinθ变形得S△AOB=
,又由
•
=|
-
|=2,可解得
2+
2=8,由基本不等式求出|
•|
|的最大值即可求出△AOB的面积最大值.及取到最大值时的夹角;
(2)在(1)的条件下,利用等号成立的条件求出角θ值,又两邻边相等,可得三角形的形状.
| 1 |
| 2 |
| a| |
| b |
| 1 |
| 2 |
(|
|
| a |
| b |
| a |
| b |
| a |
| b |
| a| |
| b |
(2)在(1)的条件下,利用等号成立的条件求出角θ值,又两邻边相等,可得三角形的形状.
解答:解:(1)由面积公式得,S△AOB=
|
•|
|sinθ变形得S△AOB=
,
又由
•
=|
-
|=2,平方整理可解得
2+
2=8,
由基本不等式
2+
2=8≥2|
•|
|,即|
•|
|≤4等号当|
=|
|时成立
故S△AOB=
≤
=
此时有S△AOB=
|
•|
|sinθ=
得sinθ=
即
与
的夹角θ=600
(2)在(1)的条件下,|
=|
|,
与
的夹角θ=600
可知此三角形是等边三角形.
| 1 |
| 2 |
| a| |
| b |
| 1 |
| 2 |
(|
|
又由
| a |
| b |
| a |
| b |
| a |
| b |
由基本不等式
| a |
| b |
| a| |
| b |
| a| |
| b |
| a| |
| b |
故S△AOB=
| 1 |
| 2 |
(|
|
| 1 |
| 2 |
| 42-4 |
| 3 |
此时有S△AOB=
| 1 |
| 2 |
| a| |
| b |
| 3 |
| ||
| 2 |
| a |
| b |
(2)在(1)的条件下,|
| a| |
| b |
| a |
| b |
可知此三角形是等边三角形.
点评:本题考查向量的运算与三角形的面积公式,及知三角函数值求角.是一道典型的三角与向量结合的好题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
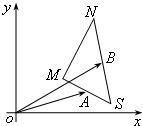 如图,已知
如图,已知