题目内容

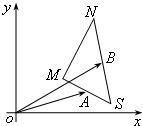精英家教网如图，已知
OA
=
a
，
OB
=
b
，对任意点M，M点关于A点的对称点为S，S点关于B点的对称点为N，用
a
、
b
表示向量
MN
．
分析：根据M点关于A点的对称点为S，S点关于B点的对称点为N，我们易得
a
=
1
2
(
OM
+
OS
)，
b
=
1
2
(
ON
+
OS
)，两式相减后，易得到向量
MN
与向量
a
、
b
的关系．
解答：解：∵M点关于A点的对称点为S
∴A为MS的中点，
又∵S点关于B点的对称点为N
∴B为SN的中点，
∴
a
=
1
2
(
OM
+
OS
)，
b
=
1
2
(
ON
+
OS
)，
两式相减得
a
-
b
=
1
2
(
OM
-
ON
)=
1
2
NM

∴
MN
=2(
b
-
a
)
点评：本题考查的知识点是向量加减混合运算及其几何意义，我们根据M点关于A点的对称点为S，S点关于B点的对称点为N，得到
a
=
1
2
(
OM
+
OS
)，
b
=
1
2
(
ON
+
OS
)，是解答本题的关键．
练习册系列答案
相关题目
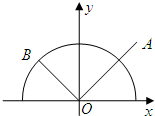精英家教网如图，已知点A（1，1）和单位圆上半部分上的动点B．
（1）若
OA
⊥
OB
，求向量
OB
；
（2）求|
OA
+
OB
|的最大值．
如图，已知
OA
=
a
，
OB
=
b
，任意点M关于点A的对称点为S，点S关于点B的对称点为N．
（1）用
a
，
b
表示向量
MN
；
（2）设|
a
|=l，|
b
|=2，
a
与
b
的夹角为30°，
MN
⊥（λ
a
+
b
），求实数λ的值．
如图，已知
OA
=
p
，
OB
=
q
，
OC
=
r
且
AB
=2
BC

（1）试用
p
，
q
表示
r
，
（2）若A(
7
2
，
1
2
)，B(
5
2
，
3
2
)，求点C的坐标．
如图，已知|
OA
|=3，|
OB
|=1，
OA
•
OB
=0，∠AOP=
π
6
，若
OP
=t
OA
+
OB
，则实数t等于（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网