题目内容
已知抛物线C:y2=2px(p>0)的焦点F与双曲线
-
=1的右焦点重合,设AB为过抛物线C焦点的弦,则|AB|的最小值为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、3 | B、6 | C、12 | D、24 |
考点:圆锥曲线的综合
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线方程可得焦点坐标,进而可设直线L的方程与抛物线联立根据韦达定理求得x1+x2,进而根据抛物线定义可求得|AB|的表达式,整理可得|AB|=12(1+
),进而可知当a=90°时AB|有最小值.
| 1 |
| k2 |
解答:
解:双曲线
-
=1的右焦点(3,0),抛物线的焦点F坐标(3,0),
可得抛物线方程为:y2=12x.
设直线L过F,斜率存在时,则直线L方程为y=k(x-3),
联立y2=12x得k2x2-(6k2+12)x+9k2=0,
由韦达定理得x1+x2=6+
,
|AB|=x1+x2+6=12+
=12(1+
)>12,
当k→∞时|AB|→12;
当a=90°时,即AB垂直于X轴时,AB=12,
综上所述,AB的最小值是12.
故选:C.
| x2 |
| 4 |
| y2 |
| 5 |
可得抛物线方程为:y2=12x.
设直线L过F,斜率存在时,则直线L方程为y=k(x-3),
联立y2=12x得k2x2-(6k2+12)x+9k2=0,
由韦达定理得x1+x2=6+
| 12 |
| k2 |
|AB|=x1+x2+6=12+
| 12 |
| k2 |
| 1 |
| k2 |
当k→∞时|AB|→12;
当a=90°时,即AB垂直于X轴时,AB=12,
综上所述,AB的最小值是12.
故选:C.
点评:本题主要考查抛物线的应用.这道题综合了抛物线的性质、抛物线的焦点弦、直线与抛物线的关系等问题.综合性很强.

练习册系列答案
相关题目
函数f(x)=
+ln
的零点所在的大致区间是( )
| 2 |
| x |
| 1 |
| x-1 |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(1,2)与(2,3) |
 如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,SA=a且
如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,SA=a且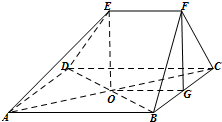 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.
如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.