题目内容
如图,O是△ABC所在平面外一点,OA、OB、OC两两垂直,∠OBA=45°,∠OBC=60°,
(1)求BC与平面OAB所成的角;
(2)求OC与平面ABC所成的角.
解:(1)OC⊥平面OAB,所以∠CBO=60°,即为所求角的大小.

(2)如图,作OH⊥平面ABC于H,连结并延长CH交AB于M,连结OM、AH、BH,则∠OBA=45°,
所以OA=OB,AH=BH.
由Rt△OAC≌Rt△OBC,得AC=BC,
所以△AHC≌△BHC,因而∠ACH=∠BCH,CM⊥AB.
由于OH⊥面ABC,所以∠OCM就是OC与平面ABC所成的角.
设OA=OB=a,则
OC=OB·tan∠OBC=![]() ,
,
OM=OB·sin∠OBA=![]() ,
,
tan∠OCM=![]() .
.
∴∠OCM=arctan![]() 即为所求.
即为所求.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 选考题
选考题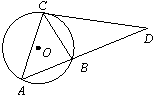 (请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)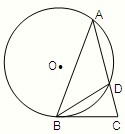 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.