题目内容
 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
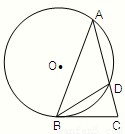
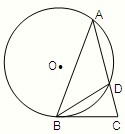
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.(1)如图,在△ABC中,AB=AC,∠C=72°,⊙O过A、B两点且与BC相切于点B,与AC交于点D,连接B、D,若BC=
| 5 |
(2)已知双曲线C:x2-y2=2,以双曲线的左焦点F为极点,射线FO(O为坐标原点)为极轴,点M为双曲线上任意一点,其极坐标是(ρ,θ),试根据双曲线的定义求出ρ与θ的关系式(将ρ用θ表示).
分析:(1)由条件可得BC=BD=DA=
-1,由切割线定理知BC2=CD•CA,解方程求得AC的长.
(2)由双曲线的方程知:a=
,b=
.c=2,e=
,
=1,分M在双曲线的左支上和M在双曲线的右支上两种情况,利用双曲线的定义求得ρ与θ的关系式.
| 5 |
(2)由双曲线的方程知:a=
| 2 |
| 2 |
| 2 |
| b2 |
| c |
解答: 解:(1)如图,由∠C=72°,AB=AC知,∠ABC=72°,∠BAC=36°.
解:(1)如图,由∠C=72°,AB=AC知,∠ABC=72°,∠BAC=36°.
由弦切角定理知∠DBC=36°,…(4分)
又∠C=72°得∠BDC=72°,∴∠ABD=72°-360=360,故BC=BD=DA=
-1,…(8分)
由切割线定理知BC2=CD•CA,即(
-1)2=[CA-(
-1)]•CA,
解得:AC=2或AC=
-3(舍),所以AC的长为2.…(12分)
(2)由双曲线的方程知:a=
,b=
.c=2,e=
,
=1,结合图形,
当M在双曲线的左支上时,
由双曲线的定义得
=e,即
=
,所以ρ=
.(6分)
当M在双曲线的右支上时,
由双曲线的定义得
=e,即
=
,所以ρ=
.(12)分
 解:(1)如图,由∠C=72°,AB=AC知,∠ABC=72°,∠BAC=36°.
解:(1)如图,由∠C=72°,AB=AC知,∠ABC=72°,∠BAC=36°.由弦切角定理知∠DBC=36°,…(4分)
又∠C=72°得∠BDC=72°,∴∠ABD=72°-360=360,故BC=BD=DA=
| 5 |
由切割线定理知BC2=CD•CA,即(
| 5 |
| 5 |
解得:AC=2或AC=
| 5 |
(2)由双曲线的方程知:a=
| 2 |
| 2 |
| 2 |
| b2 |
| c |
当M在双曲线的左支上时,
由双曲线的定义得
| ρ | ||
|
| ρ |
| 1-ρcosθ |
| 2 |
| ||
1+
|
当M在双曲线的右支上时,
由双曲线的定义得
| ρ | ||
ρcosθ-
|
| ρ |
| ρcosθ-1 |
| 2 |
| ||
|
点评:本题主要考查与圆相关的比例线段,把极坐标方程化为直角坐标方程的方法,双曲线的简单性质的应用,属于中档题.

练习册系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)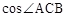 的值为 _____.
的值为 _____.
 的圆心的极坐标是 _____.
的圆心的极坐标是 _____. 的解集为 _____.
的解集为 _____.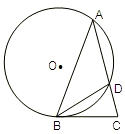 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.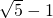 ,求AC的长.
,求AC的长. ,求AC的长.
,求AC的长.