题目内容
如图所示，O是△ABC的内心，∠BOC=100°，则∠BAC=
分析：由三角形内切定义可知：OB、OC是∠ABC、∠ACB的角平分线．利用内角和定理先求得∠OBC+∠OCB=80°，所以可知∠OBC+∠OCB=
（∠ABC+∠ACB），把对应数值代入此关系式即可求得∠BAC的值．
| 1 |
| 2 |
解答：解：∵OB、OC是∠ABC、∠ACB的角平分线，
∴∠OBC+∠OCB=180°-100°=80°，而∠OBC+∠OCB=
（∠ABC+∠ACB）=80°，
∴∠ABC+∠ACB=160°，
∴∠BAC=180°-160°=20°．
故答案为20．
∴∠OBC+∠OCB=180°-100°=80°，而∠OBC+∠OCB=
| 1 |
| 2 |
∴∠ABC+∠ACB=160°，
∴∠BAC=180°-160°=20°．
故答案为20．
点评：本题通过三角形内切圆，考查切线的性质．属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
A．（选修4-4坐标系与参数方程）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）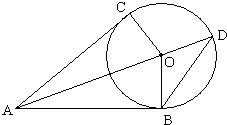
（2011•广东模拟）（几何证明选讲）如图所示，AC和AB分别是圆O的切线，B、C 为切点，且OC=3，AB=4，延长OA到D点，则△ABD的面积是
。