题目内容
已知椭圆C:  +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为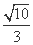 时,求k的值.
时,求k的值.
解:(1)由题设知,椭圆焦点在x轴上,
∴a=2.
由e= =
= 得c=
得c=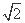 ,
,
∴b2=a2-c2=2.
∴椭圆C的方程为 +
+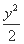 =1.
=1.
(2)由 消去y,
消去y,
整理得(1+2k2)x2-4k2x+2k2-4=0.
设M(x1,y1),N(x2,y2).
则Δ=(-4k2)2-4(1+2k2)(2k2-4)>0(※)
且x1+x2= ,x1·x2=
,x1·x2= ,
,
∴|MN|=
=
=
=
=
设点A(2,0)到直线y=k(x-1)的距离为d,
则d= .
.
∴S△AMN= |MN|·d=
|MN|·d= =
=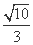 ,
,
解得k=±1,
代入(※)式成立,∴k=±1.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
已知椭圆C:  +
+ =1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=
=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF= ,则C的离心率为( )
,则C的离心率为( )
(A)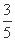 (B)
(B)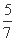 (C)
(C) (D)
(D)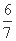
某单位有2 000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
(3)若要抽20人调查对2016年巴黎奥运会筹备情况的了解,则应怎样抽样?
 )时,f(x)=sin πx,f
)时,f(x)=sin πx,f =0,则函数f(x)在区间[0,6]上的零点个数是( )
=0,则函数f(x)在区间[0,6]上的零点个数是( )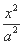 -
-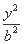 =1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且
=1(a>0,b>0)的左焦点,B1B2是双曲线的虚轴,M是OB1的中点,过F、M的直线与双曲线C的一个交点为A,且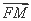 =2
=2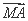 ,则双曲线C离心率是 .
,则双曲线C离心率是 .  (x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .
(x+c)与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .  +
+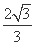 ).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点.
).过点P(1,1)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N分别为线段AB,CD的中点. +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.