题目内容
本小题满分12分)
已知 函数f (x)=
函数f (x)= x3+ ax2-bx (a, b∈R) .
x3+ ax2-bx (a, b∈R) .
(1)若y=f (x)图象上的点(1,-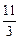 )处的切线斜率为-4
)处的切线斜率为-4 ,求y=f (x)的极大值;
,求y=f (x)的极大值;
(2)若y=f (x)在区间[-1,2]上是单调减函数,求a + b的最小值.

已知
 函数f (x)=
函数f (x)= x3+ ax2-bx (a, b∈R) .
x3+ ax2-bx (a, b∈R) .(1)若y=f (x)图象上的点(1,-
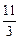 )处的切线斜率为-4
)处的切线斜率为-4 ,求y=f (x)的极大值;
,求y=f (x)的极大值;(2)若y=f (x)在区间[-1,2]上是单调减函数,求a + b的最小值.
解:(1)∵f ′(x)=x2+2ax-b ,
∴ 由题意可 知:f ′(1)=-4且f (1)=-
知:f ′(1)=-4且f (1)=-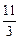 ,
,
∴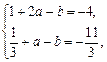 解得:
解得: …………………………2分
…………………………2分
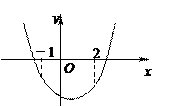
∴ f (x)= x3-x2-3x。
x3-x2-3x。
f ′(x)=x2-2x-3=(x+1)(x-3).
令f ′(x)= 0,得x1=-1,x2=3,……………3分
0,得x1=-1,x2=3,……………3分
由此可知:
∴ 当x=-1时, f (x)取极大值 . …………………………6分
. …………………………6分
(2) ∵y=f (x)在区间[-1,2]上是单调减函数,
∴f ′(x)=x2+2ax-b≤0在区间[-1,2]上恒成立.
根据二次函数图象可知f ′(-1)≤0且f ′(2)≤0,即:
 也即
也即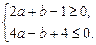 …………………9分
…………………9分

作出不等式组表示的平面区域如图:
当直线z=a +b经过交点P(-
+b经过交点P(-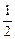 , 2)时,
, 2)时,
z=a+b取得最小值z=-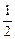 +2=
+2= ,
,
∴z=a+b取得最小值为 ……………………12分
……………………12分
∴ 由题意可
 知:f ′(1)=-4且f (1)=-
知:f ′(1)=-4且f (1)=-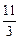 ,
,∴
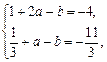 解得:
解得: …………………………2分
…………………………2分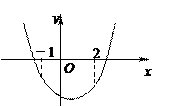
∴ f (x)=
 x3-x2-3x。
x3-x2-3x。f ′(x)=x2-2x-3=(x+1)(x-3).
令f ′(x)=
 0,得x1=-1,x2=3,……………3分
0,得x1=-1,x2=3,……………3分由此可知:
| x | (-∞,-1) | -1 | (-1, 3) | 3 | (3, +∞) |
| f ’(x) | + | 0 | - | 0 | + |
| f (x) | ↗ | f (x)极大5/3 | ↘ | f (x) 极小 | ↗ |
 . …………………………6分
. …………………………6分(2) ∵y=f (x)在区间[-1,2]上是单调减函数,
∴f ′(x)=x2+2ax-b≤0在区间[-1,2]上恒成立.
根据二次函数图象可知f ′(-1)≤0且f ′(2)≤0,即:
 也即
也即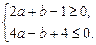 …………………9分
…………………9分
作出不等式组表示的平面区域如图:
当直线z=a
 +b经过交点P(-
+b经过交点P(-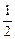 , 2)时,
, 2)时,z=a+b取得最小值z=-
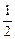 +2=
+2= ,
,∴z=a+b取得最小值为
 ……………………12分
……………………12分略

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 .
.  在区间
在区间 上的最大值和最小值。
上的最大值和最小值。 .
. 存在单调增区间,求
存在单调增区间,求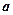 的取值范围;
的取值范围;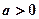 ,使得方程
,使得方程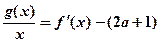 在区间
在区间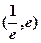 内有且只有两个不相等的实数根?若存在,求出
内有且只有两个不相等的实数根?若存在,求出 ,且
,且 ,其中
,其中 是自然对数的底数.
是自然对数的底数. 与
与 的关系;
的关系; 在其定义域内为单调函数,求
在其定义域内为单调函数,求 在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以
在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以 的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s)
的速度与A同向运动,问两物体何时相遇?相遇时物体A的走过的路程是多少?(时间单位为:s,速度单位为:m/s) 要在公园内建一块顶点都在圆P上的多边形活动场地.
要在公园内建一块顶点都在圆P上的多边形活动场地.
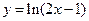 上的点到直线
上的点到直线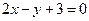 的最短距离是 .
的最短距离是 .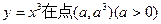 处的切线与x轴、直线
处的切线与x轴、直线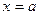 所围成的三角形的面积为
所围成的三角形的面积为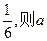 = .
= . B (log2x)′=
B (log2x)′=