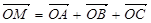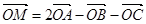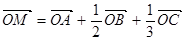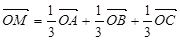题目内容
设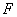 为抛物线
为抛物线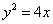 的焦点,
的焦点, 、
、 、
、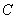 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则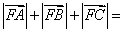 ( )
( )
| A.9 | B.6 | C.4 | D.3 |
B
解析试题分析:先设A(x1,y1),B(x2,y2),C(x3,y3),根据抛物线方程求得焦点坐标和准线方程,再依据 判断点F是△ABC重心,进而可求x1+x2+x3的值.最后根据抛物线的定义求得答案解:设A(x1,y1),B(x2,y2),C(x3,y3),抛物线焦点坐标F(1,0),准线方程:x=-1,∵
判断点F是△ABC重心,进而可求x1+x2+x3的值.最后根据抛物线的定义求得答案解:设A(x1,y1),B(x2,y2),C(x3,y3),抛物线焦点坐标F(1,0),准线方程:x=-1,∵ ,∴点F是△ABC重心,则x1+x2+x3=3,y1+y2+y3=0,而|FA|=x1-(-1)=x1+1,|FB|=x2-(-1)=x2+1,|FC|=x3-(-1)=x3+1,∴|FA|+|FB|+|FC|=x1+1+x2+1+x3+1=(x1+x2+x3)+3=3+3=6,故选B
,∴点F是△ABC重心,则x1+x2+x3=3,y1+y2+y3=0,而|FA|=x1-(-1)=x1+1,|FB|=x2-(-1)=x2+1,|FC|=x3-(-1)=x3+1,∴|FA|+|FB|+|FC|=x1+1+x2+1+x3+1=(x1+x2+x3)+3=3+3=6,故选B
考点:抛物线的简单性质
点评:本题主要考查了抛物线的简单性质.解本题的关键是判断出F点为三角形的重心.

练习册系列答案
相关题目
若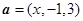 ,
,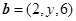 ,且
,且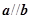 ,则 ( )
,则 ( )
A.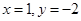 | B.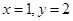 |
C.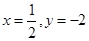 | D.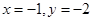 |
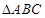 中,
中,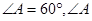 的平分线
的平分线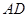 交边
交边 于
于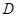 ,已知
,已知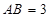 ,且
,且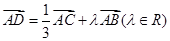 ,则
,则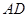 的长为 ( )
的长为 ( )
| A.1 | B. | C. | D.3 |
已知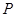 是
是 所在平面内一点,
所在平面内一点,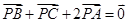 ,现将一粒红豆随机撒在
,现将一粒红豆随机撒在 内,则红豆落在
内,则红豆落在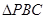 内的概率是( )
内的概率是( )
A.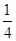 | B.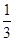 | C.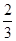 | D.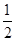 |
在△ABC中,若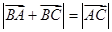 ,则△ABC的形状为( )
,则△ABC的形状为( )
| A.等腰三角形 | B.直角三角形 | C.等腰直角三角形 | D.不能确定 |
设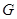 为△
为△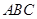 的重心,且
的重心,且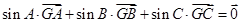 ,则
,则 的大小为( )
的大小为( )
| A.450 | B.600 | C.300 | D.150 |
空间直角坐标系中,O为坐标原点,已知两点坐标为A(3,1,0),B(-1,3,0),若点C满足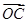 =
=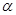
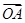 +
+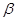
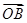 ,其中
,其中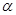 ,
,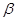 ∈R,
∈R,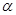 +
+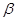 =1,则点C的轨迹为
=1,则点C的轨迹为
| A.平面 | B.直线 | C.圆 | D.线段 |
在四边形 中,
中,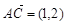 ,
,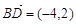 ,则该四边形的面积为( )
,则该四边形的面积为( )
A.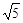 | B.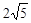 | C.5 | D.10 |
 ,下列条件中能确定的M与点A、B、C一定共面的是( )
,下列条件中能确定的M与点A、B、C一定共面的是( )