题目内容
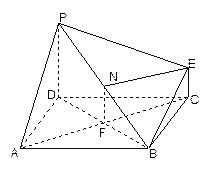
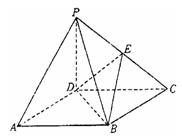
(本小题满分14分)下图为一简单组合体,其底面ABCD为正方形,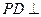 平面
平面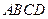 ,
,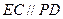 ,且
,且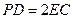 ,
,
(1)求证:BE//平面PDA;
(2)若N为线段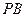 的中点,求证:
的中点,求证: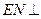 平面
平面 ;
;
(3)若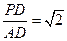 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.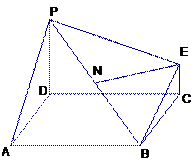
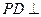 平面
平面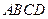 ,
,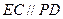 ,且
,且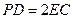 ,
, (1)求证:BE//平面PDA;
(2)若N为线段
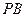 的中点,求证:
的中点,求证: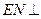 平面
平面 ;
;(3)若
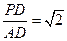 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.
(1)证明略;
(2)证明略;
(3)45°
(2)证明略;
(3)45°
(1)证明:∵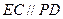 ,
, 平面
平面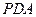 ,
,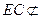 平面
平面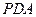
∴EC//平面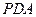 ,同理可得BC//平面
,同理可得BC//平面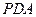 ----------------------------------------2分
----------------------------------------2分
∵EC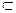 平面EBC,BC
平面EBC,BC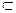 平面EBC且
平面EBC且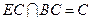
∴平面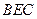 //平面
//平面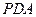 -----------------------------------------------------------------3分
-----------------------------------------------------------------3分
又∵BE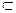 平面EBC ∴BE//平面PDA-----------------------------------------------------4分
平面EBC ∴BE//平面PDA-----------------------------------------------------4分
(2)证法1:连结AC与BD交于点F, 连结NF,
∵F为BD的中点,
∴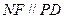 且
且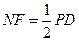 ,--------------------------6分
,--------------------------6分
又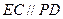 且
且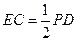
∴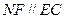 且
且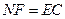
∴四边形NFCE为平行四边形-------------------------7分
∴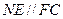
∵
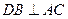 ,
,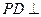 平面
平面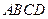 ,
,
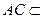 面
面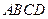 ∴
∴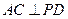 ,
,
又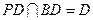
∴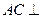 面
面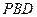 ∴
∴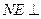 面
面 ----------------------------------------9分
----------------------------------------9分
证法2:如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:设该简单组合体的底面边长为1,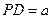
则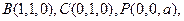
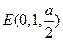 ,
,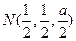 --------------------------------6分
--------------------------------6分
∴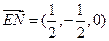 ,
,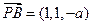 ,
,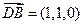
∵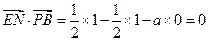 ,
, ,
,
∴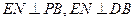 ---------------------------------8分
---------------------------------8分
∵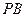 、
、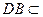 面
面 ,且
,且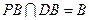
∴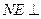 面
面 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分
(3)解法1:连结DN,由(2)知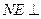 面
面
∴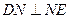 , ∵
, ∵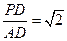 ,
,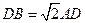 ∴
∴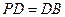 ∴
∴
∴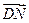 为平面PBE的法向量,设
为平面PBE的法向量,设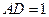 ,则
,则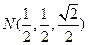 ∴
∴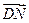 =
=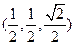 ---11分
---11分
∵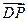 为平面ABCD的法向量,
为平面ABCD的法向量,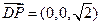 ,---------------------------------------------12分
,---------------------------------------------12分
设平面PBE与平面ABCD所成的二面角为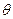 ,
,
则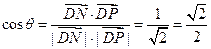 ------------------------------------------------13分
------------------------------------------------13分
∴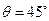 即平面PBE与平面ABCD所成的二面角为45°--------------------14分
即平面PBE与平面ABCD所成的二面角为45°--------------------14分
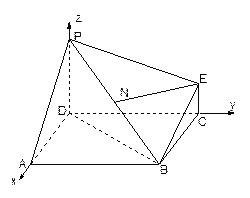
解法2:延长PE与DC的延长线交于点G,连结GB,
则GB为平面PBE与ABCD的交线--------------------10分
∵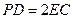 ∴
∴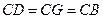
∴D、B、G在以C为圆心、以BC为半径的圆上,
∴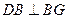 -------------------11分
-------------------11分
∵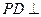 平面
平面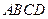 ,
,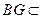 面
面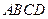
∴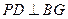 且
且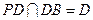
∴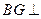 面
面 ∵
∵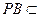 面
面
∴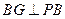
∴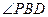 为平面PBE与平面ABCD所成的二面角的平面角----------------------------13分
为平面PBE与平面ABCD所成的二面角的平面角----------------------------13分
在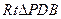 中 ∵
中 ∵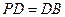
∴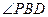 =45°即平面PBE与平面ABCD所成的二面角为45°----------------14分
=45°即平面PBE与平面ABCD所成的二面角为45°----------------14分
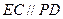 ,
, 平面
平面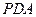 ,
,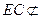 平面
平面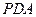
∴EC//平面
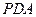 ,同理可得BC//平面
,同理可得BC//平面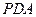 ----------------------------------------2分
----------------------------------------2分∵EC
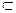 平面EBC,BC
平面EBC,BC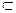 平面EBC且
平面EBC且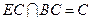
∴平面
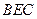 //平面
//平面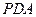 -----------------------------------------------------------------3分
-----------------------------------------------------------------3分又∵BE
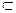 平面EBC ∴BE//平面PDA-----------------------------------------------------4分
平面EBC ∴BE//平面PDA-----------------------------------------------------4分(2)证法1:连结AC与BD交于点F, 连结NF,
∵F为BD的中点,
∴
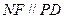 且
且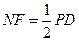 ,--------------------------6分
,--------------------------6分又
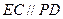 且
且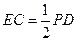
∴
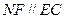 且
且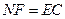
∴四边形NFCE为平行四边形-------------------------7分
∴
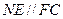
∵

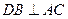 ,
,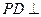 平面
平面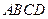 ,
,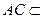 面
面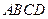 ∴
∴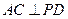 ,
,又
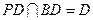
∴
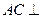 面
面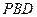 ∴
∴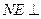 面
面 ----------------------------------------9分
----------------------------------------9分
证法2:如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:设该简单组合体的底面边长为1,
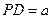
则
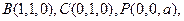
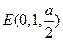 ,
,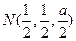 --------------------------------6分
--------------------------------6分∴
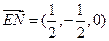 ,
,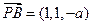 ,
,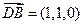
∵
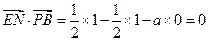 ,
, ,
,∴
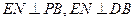 ---------------------------------8分
---------------------------------8分∵
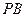 、
、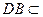 面
面 ,且
,且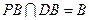
∴
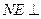 面
面 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分(3)解法1:连结DN,由(2)知
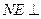 面
面
∴
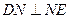 , ∵
, ∵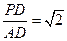 ,
,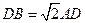 ∴
∴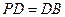 ∴
∴
∴
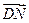 为平面PBE的法向量,设
为平面PBE的法向量,设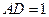 ,则
,则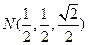 ∴
∴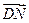 =
=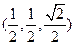 ---11分
---11分∵
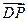 为平面ABCD的法向量,
为平面ABCD的法向量,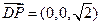 ,---------------------------------------------12分
,---------------------------------------------12分设平面PBE与平面ABCD所成的二面角为
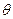 ,
,则
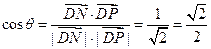 ------------------------------------------------13分
------------------------------------------------13分∴
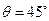 即平面PBE与平面ABCD所成的二面角为45°--------------------14分
即平面PBE与平面ABCD所成的二面角为45°--------------------14分解法2:延长PE与DC的延长线交于点G,连结GB,
则GB为平面PBE与ABCD的交线--------------------10分
∵
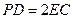 ∴
∴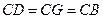
∴D、B、G在以C为圆心、以BC为半径的圆上,
∴
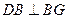 -------------------11分
-------------------11分∵
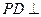 平面
平面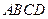 ,
,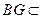 面
面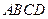
∴
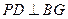 且
且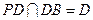
∴
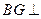 面
面 ∵
∵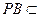 面
面
∴
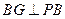
∴
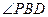 为平面PBE与平面ABCD所成的二面角的平面角----------------------------13分
为平面PBE与平面ABCD所成的二面角的平面角----------------------------13分在
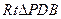 中 ∵
中 ∵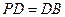
∴
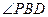 =45°即平面PBE与平面ABCD所成的二面角为45°----------------14分
=45°即平面PBE与平面ABCD所成的二面角为45°----------------14分


练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
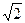 ,CD=1
,CD=1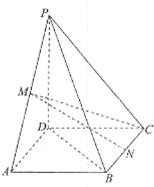
 中,
中, ,
,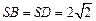 ,底面
,底面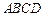 是菱形,且
是菱形,且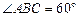 ,
,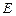 为
为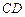 的中点.
的中点.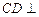 平面
平面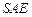 ;
;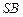 上是否存在点
上是否存在点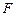 ,使得
,使得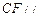 平面
平面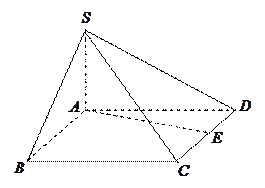
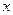
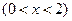 的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.
的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.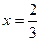 时,Vl取最大值
时,Vl取最大值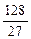 ,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。
,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。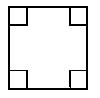
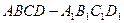 中,底面是边长为2的正方形,
中,底面是边长为2的正方形,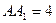 .
.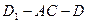 的平面角,并求出它的正切值;
的平面角,并求出它的正切值;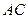 与
与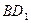 所成的角.
所成的角.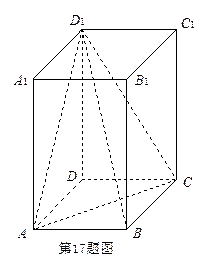
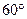 圈上有A、B两点,它们的经度相差
圈上有A、B两点,它们的经度相差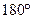 ,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )
,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )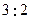 B.
B. 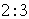 C.
C. 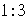 D.
D. 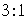
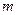 ,
, 和平面
和平面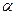 ,
,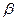 ,
,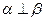 的一个充分条件是( )
的一个充分条件是( )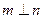 ,
,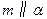 ,
,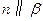
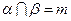 ,
,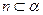
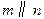 ,
,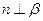 ,
,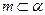
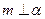 ,
,