Question

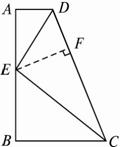
如图2-2-9,已知四边形ABCD内接于⊙O,边AB与DC的延长线交于点E,边AD与BC的延长线相交于点F,EG与FG分别是∠AEC和∠AFC的角平分线.求证:EG⊥FG.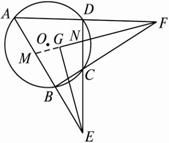

图2-2-9

Answer 1

思路分析:注意到EG平分∠AED,因此，要证GF⊥GE,只要构造等腰三角形，便可利用三线合一的性质来证.

证明:延长FG交AB于M,?

∵四边形ABCD内接于⊙O,?

∴∠NCF =∠A.?

∵∠MNE =∠NFC+∠NCF,?

∴∠MNE =∠NFC+∠A.?

又FG平分∠AFB,?

∴∠AFM =∠NFC.?

∴∠MNE =∠A+∠AFM.?

又∠NME =∠A+∠AFM,?

∴∠MNE =∠NME,即EM =EN.?

又∵GE平分∠MEN,∴GE⊥MN,?

即EG⊥FG.