题目内容
如图2-3-9,已知直角梯形ABCD中,∠A =∠B=90°,AD∥BC,E为AB上一点,DE平分∠ADC,CE平分∠BCD.求证:以AB为直径的圆与DC相切.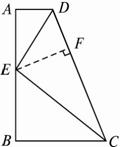
图2-3-9
思路分析:要证以AB为直径的圆与直线DC相切,只要证AB中点(圆心)到直线DC距离等于半径(AB的一半),先证E为AB中点,再证E到DC距离等于
AB.
证明:过E作EF⊥DC,垂足为F.?
∵ED平分∠ADC,DA⊥EA,EF⊥DF,?
∴EA =EF.?
同理,EB =EF,∴EB =EA,?
即E为AB中点.?
又EF =EA =EB =
,?
∴以AB为直径的圆与DC相切.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
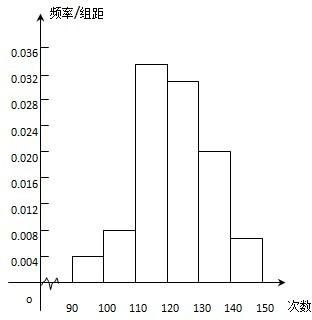
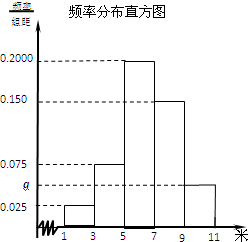为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成[1，3），[3，5），[5，7），[7，9），[9，11）五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
