Question

如图2-2-6所示，在△ABC中，AB=AC，延长CA到P，再延长AB到Q，使得AP=BQ.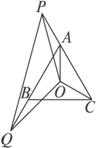

图2-2-6

求证：△ABC的外心O与A、P、Q四点共圆.

Answer 1

思路分析：要证O、A、P、Q四点共圆，只需证∠CPO=∠AQO即可.为此，只要证△CPO≌△AQO即可.

证明：连结OA、OC、OP、OQ.

在△OCP和△OAQ中，OC=OA，

由已知,CA=AB，AP=BQ，

∴CP=AQ.

又O是△ABC的外心，

∴∠OCP=∠OAC.

由于等腰三角形的外心在顶角的平分线上，

∴∠OAC=∠OAQ，从而∠OCP=∠OAQ.

∴△OCP≌△OAQ.

∴∠CPO=∠AQO.

∴O、A、P、Q四点共圆.

    深化升华 本题也可证△OAP≌△OBQ,得到角相等，进而说明四点共圆.你可以试着写出另一种证明.