题目内容
已知 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
A
解析试题分析:因为 为等比数列, 且
为等比数列, 且 ,所以
,所以 ,又
,又 ,联立解得:
,联立解得: ,所以
,所以 ,所以
,所以 -7.
-7.
考点:等比数列的性质
点评:此题主要考查等比数列的性质。在学习中,我们要把等比数列的性质和等差数列的性质进行比较、区分着记忆。以免混淆。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列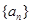 的首项为1,数列
的首项为1,数列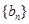 为等比数列且
为等比数列且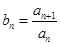 ,若
,若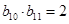 ,则
,则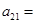 ( )
( )
| A.20 | B.512 | C.1013 | D.1024 |
已知等差数列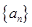 的前项和为
的前项和为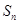 ,且
,且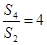 ,则
,则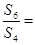 ( )
( )
A.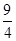 | B.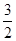 | C.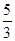 | D.4 |
已知正项等比数列 中,
中, ,
, ,则
,则
| A.2 | B. | C. | D. |
等比数列x,3x+3,6x+6,…的第四项等于( )
| A.-24 | B.0 | C.12 | D.24 |
在各项均为正数的数列 中,对任意
中,对任意 都有
都有 .若
.若 ,则
,则 等于( )
等于( )
| A.256 | B.510 | C.512 | D.1024 |
已知各项均为正数的等比数列{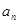 },
},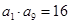 ,则
,则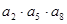 的值为( )
的值为( )
| A.16 | B.32 | C.48 | D.64 |
在等比数列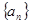 中,
中, ,
, 则数列的公比
则数列的公比 为 ( )
为 ( )
A. | B. | C. | D. |
已知等比数列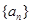 中有
中有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则
| A.2 | B.4 | C.8 | D.16 |