题目内容
在各项均为正数的数列 中,对任意
中,对任意 都有
都有 .若
.若 ,则
,则 等于( )
等于( )
| A.256 | B.510 | C.512 | D.1024 |
C
解析试题分析:利用am+n=am•an.求出a12,a3,列出a6,a9的关系,求出a9的值.解:在各项均为正数的数列{an}中,对任意m,n∈N*都有am+n=am•an.所以a12=a6•a6=642,又a6=a3•a3,∴a3=8,∴a12=a9•a3,解得a9= =512.故选C
=512.故选C
考点:数列递推关系式
点评:本题考查数列递推关系式的应用,注意各项均为正数的数列条件的应用,考查计算能力.

练习册系列答案
相关题目
在各项都为正数的等比数列 中,首项为3,前3项和为21,则
中,首项为3,前3项和为21,则 等于( )
等于( )
| A.15 | B.12 | C.9 | D.6 |
设等比数列 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知数列{ }满足
}满足 ,且
,且 ,则
,则 的值是
的值是
A. | B. | C.5 | D. |
已知 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知等比数列 中,
中,  ,
, ,则
,则 =( )
=( )
| A.64 | B.128 | C.256 | D.512 |
已知数列{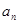 }的通项公式是
}的通项公式是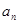 =
= (
( ),则数列的第5项为( )
),则数列的第5项为( )
A. | B. | C. | D. |
在等比数列中,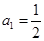 ,
,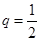 ,
,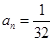 ,则项数
,则项数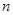 为 ( )
为 ( )
| A.3 | B.4 | C.5 | D.6 |
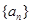 的公比
的公比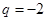 ,则
,则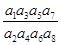 等于( )
等于( )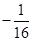 B
B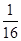 C
C D.
D. 