题目内容
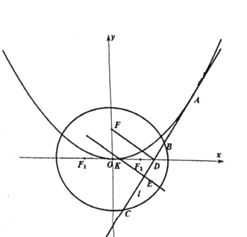
【题目】给定椭圆![]() :
:![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“伴椭圆”,若椭圆
的“伴椭圆”,若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上一个端点到
,其短轴上一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的“伴随圆”
的“伴随圆”![]() 的动弦
的动弦![]() ,过点
,过点![]() 、
、![]() 分别作“伴随圆”
分别作“伴随圆”![]() 的切线,设两切线交于点
的切线,设两切线交于点![]() ,证明:点
,证明:点![]() 的轨迹是直线,并写出该直线的方程;
的轨迹是直线,并写出该直线的方程;
(3)设点![]() 是椭圆
是椭圆![]() 的“伴随圆”
的“伴随圆”![]() 上的一个动点,过点
上的一个动点,过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() 、
、![]() ,试判断直线
,试判断直线![]() 、
、![]() 是否垂直?并说明理由.
是否垂直?并说明理由.
【答案】(1)![]() ;
;
(2)见解析;
(3)见解析.
【解析】
(1)由题意可得,![]() ,则
,则![]() ,从而得到椭圆C的方程;
,从而得到椭圆C的方程;
(2)根据题意,求得![]() ,分直线的斜率存在与不存在两种情况,将斜率存在时求得的直线,对斜率不存在时求得的点P的坐标进行检验,最后求得结果.
,分直线的斜率存在与不存在两种情况,将斜率存在时求得的直线,对斜率不存在时求得的点P的坐标进行检验,最后求得结果.
(3)讨论当P在直线![]() 上时,设出直线方程,联立椭圆方程,消去
上时,设出直线方程,联立椭圆方程,消去![]() ,得到关于
,得到关于![]() 的方程,运用判别式为0,化简整理,得到关于
的方程,运用判别式为0,化简整理,得到关于![]() 的方程,求出连根之积,判断是否为
的方程,求出连根之积,判断是否为![]() ,即可判断
,即可判断![]() 垂直.
垂直.
(1)依题意得:![]() ,所以
,所以![]() ,
,
所以椭圆方程为:![]() ;
;
(2)由题意可得伴随圆的方程为![]() ,
,
点![]() 为
为![]() ,所以
,所以![]() ,
,
当过点P的直线斜率不存在时,则![]() ,
,
可求得![]() ,此时
,此时![]() ,
,
当过点P的直线斜率存在时,设直线方程为:![]() ,
,
设![]() ,
,![]() ,
,
则经过各自的切线方程为: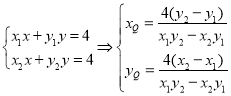 ,
,
把 代入,解得
代入,解得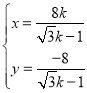 ,
,
消![]() ,得到
,得到![]() ,
,
当![]() 不存在时,
不存在时,![]() 也满足方程
也满足方程![]() ,
,
所以点![]() 的轨迹是一条直线,且方程为
的轨迹是一条直线,且方程为![]() ;
;
(3)当![]() 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设![]() 无斜率,
无斜率,
因为![]() 与椭圆只有一个公共点,则其方程为:
与椭圆只有一个公共点,则其方程为:![]() ,此时经过点
,此时经过点![]() 或
或![]() ,
,
则直线![]() 的方程为:
的方程为:![]() ,经检验,满足垂直关系;
,经检验,满足垂直关系;
当![]() 斜率都存在时,设点
斜率都存在时,设点![]() ,
,
因为点P在伴随圆上,所以有![]() ,
,
设经过点![]() ,且与椭圆只有一个公共点的直线方程为:
,且与椭圆只有一个公共点的直线方程为:![]() ,
,
联立椭圆方程,
 ,消
,消![]() 化简得
化简得![]() ,
,
因为相切,所以![]() ,即:
,即:![]() ,
,
又因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以直线![]() ,
,
从而得证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目