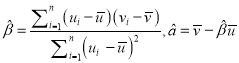题目内容
【题目】如图,在下列三个正方体![]() 中,
中,![]() 均为所在棱的中点,过
均为所在棱的中点,过![]() 作正方体的截面.在各正方体中,直线
作正方体的截面.在各正方体中,直线![]() 与平面
与平面![]() 的位置关系描述正确的是
的位置关系描述正确的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
【答案】A
【解析】
①连结![]() ,根据面面平行的判定定理可证平面
,根据面面平行的判定定理可证平面![]() 平面
平面![]() ,进而可得
,进而可得![]() 平面
平面![]() ;
;
②③都可以根据线面垂直的判定定理,用向量的方法分别证明![]() ,
,![]() ,即可证明
,即可证明![]() 平面
平面![]() ;从而可得出结果.
;从而可得出结果.
①连结![]() ,因为
,因为![]() 均为所在棱的中点,所以
均为所在棱的中点,所以![]() ,
,![]() ,从而可得
,从而可得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;根据
;根据![]() ,可得平面
,可得平面![]() 平面
平面![]() ;所以
;所以![]() 平面
平面![]() ;
;
②设正方体棱长为![]() ,因为
,因为![]() 均为所在棱的中点,
均为所在棱的中点,
所以 ,即
,即![]() ;
;
又 ,即
,即![]() ;
;
又![]() ,所以
,所以![]() 平面
平面![]() ;
;
③设正方体棱长为![]() ,因为
,因为![]() 均为所在棱的中点,
均为所在棱的中点,
所以 ,即
,即![]() ;
;
又 ,即
,即![]() ;
;
又![]() ,所以
,所以![]() 平面
平面![]() ;
;
故选A

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目