题目内容
已知各项都为正数的等比数列{an}中,a1a5-2a3a5+a3a7=36,a2a4+2a2a6+a4a6=100,求数列的通项公式.
解:由已知条件a1a5-2a3a5+a3a7=36,
a2a4+2a2a6+a4a6=100,
知
∴ 即
即 ①或
①或 ②
②
解①得a3=8,a5=2.
∴q=![]() =
=![]() ,an=a3(
,an=a3(![]() )n-3=(
)n-3=(![]() )n-6.
)n-6.
解②得a3=2,a5=8.
∴q=![]() =2,an=a3·2n-3=2n-2.
=2,an=a3·2n-3=2n-2.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是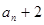 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈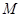 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?