题目内容
已知△ABC中,O为外心,H为垂心,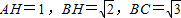 ,
,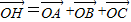 ,则S△AOB:S△BOC:S△AOC=( )
,则S△AOB:S△BOC:S△AOC=( )A.
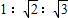
B.
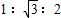
C.
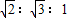
D.

【答案】分析:过点O作垂线OD交BC与点D,并延长使得OE=2OD,根据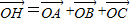 可得
可得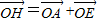 则四边形OAHE为平行四边形,从而可求出OB的长和S△BOC,然后根据
则四边形OAHE为平行四边形,从而可求出OB的长和S△BOC,然后根据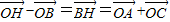 ,两边平方可求出∠AOC,从而可求出S△AOC,根据∠AOB=360°-∠BOC-∠AOC,可求出S△AOB,即可求出所求.
,两边平方可求出∠AOC,从而可求出S△AOC,根据∠AOB=360°-∠BOC-∠AOC,可求出S△AOB,即可求出所求.
解答:解: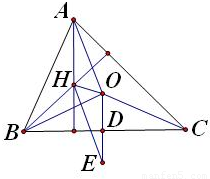 过点O作垂线OD交BC与点D,并延长使得OE=2OD
过点O作垂线OD交BC与点D,并延长使得OE=2OD
∵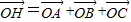 ,
,
∴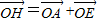 则四边形OAHE为平行四边形
则四边形OAHE为平行四边形
则AH=OE=1即OD= OE=
OE=
∵BC=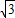
∴S△BOC= ×
×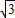 ×
× =
=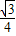
∵OD= ,BD=
,BD=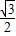
∴OA=OB=OC=1
∵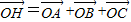 ,
,
∴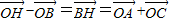
则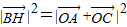 即2=1+1+2cos∠AOC
即2=1+1+2cos∠AOC
∴∠AOC=90°
而S△BOC=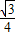 =
= sin∠BOC
sin∠BOC
则∠BOC=120°,∠AOB=360°-90°-120°=150°
∴S△AOB= sin∠AOB=
sin∠AOB= ×
× =
=
S△AOC= sin∠AOC=
sin∠AOC= ×1=
×1=
∴S△AOB:S△BOC:S△AOC= :
: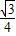 :
: =1:
=1: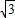 :2
:2
故选B.
点评:本题主要考查了平面向量及应用,以及三角形的垂心和外心,同时考查了运算求解的能力,属于难题.
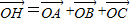 可得
可得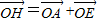 则四边形OAHE为平行四边形,从而可求出OB的长和S△BOC,然后根据
则四边形OAHE为平行四边形,从而可求出OB的长和S△BOC,然后根据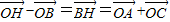 ,两边平方可求出∠AOC,从而可求出S△AOC,根据∠AOB=360°-∠BOC-∠AOC,可求出S△AOB,即可求出所求.
,两边平方可求出∠AOC,从而可求出S△AOC,根据∠AOB=360°-∠BOC-∠AOC,可求出S△AOB,即可求出所求.解答:解:
 过点O作垂线OD交BC与点D,并延长使得OE=2OD
过点O作垂线OD交BC与点D,并延长使得OE=2OD∵
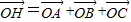 ,
,∴
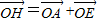 则四边形OAHE为平行四边形
则四边形OAHE为平行四边形则AH=OE=1即OD=
 OE=
OE=
∵BC=
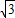
∴S△BOC=
 ×
×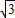 ×
× =
=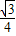
∵OD=
 ,BD=
,BD=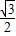
∴OA=OB=OC=1
∵
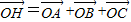 ,
,∴
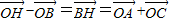
则
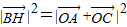 即2=1+1+2cos∠AOC
即2=1+1+2cos∠AOC∴∠AOC=90°
而S△BOC=
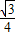 =
= sin∠BOC
sin∠BOC则∠BOC=120°,∠AOB=360°-90°-120°=150°
∴S△AOB=
 sin∠AOB=
sin∠AOB= ×
× =
=
S△AOC=
 sin∠AOC=
sin∠AOC= ×1=
×1=
∴S△AOB:S△BOC:S△AOC=
 :
: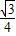 :
: =1:
=1: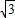 :2
:2故选B.
点评:本题主要考查了平面向量及应用,以及三角形的垂心和外心,同时考查了运算求解的能力,属于难题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
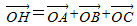 ,则S△AOB:S△BOC:S△AOC=( )
,则S△AOB:S△BOC:S△AOC=( )