题目内容

（2013•蓟县二模）已知△ABC中的重心为O，直线MN过重心O，交线段AB于M，交线段AC于N其中
AM
=m
AB
，
AN
=n
AC
，且
AO
=λ
AB
+μ
AC
，其中λ，μ为实数．则6m+3n的最小值为
3+2
2
3+2
2
．
分析：利用重心定理和向量共线定理、向量运算法则即可得出．
解答：解：如图所示，
设线段BC的中点为D，则
AO
=
2
3
AD
，
AD
=
1
2
(
AB
+
AC
)，∴
AO
=
1
3
AB
+
1
3
AC
，
①当MN∥BC时，m=n=
2
3
，∴6m+3n=6．
②当MN与BC不平行时，m，n≠
2
3
．由题意可知
1
2
≤m≤1．
设
OM
=s
MN
，
MN
=
AN
-
AM
，∴
OM
=s(
AN
-
AM
)=sm
AB
-sn
AC

则m
AB
=
AM
=
AO
+
OM
=
1
3
AB
+
1
3
AC
+sm
AB
-sn
AC
=(
1
3
+sm)
AB
+(
1
3
-sn)
AC
．
∴
m=
1
3
+sm
0=
1
3
-sn
，化为n=
m
3m-1

则6m+3n=6m+
3m
3m-1
=2(3m-1)+
1
3m-1
+3≥2
2(3m-1)•
1
3m-1
+3=3+2
2
，当且仅当
2+
2
6
时取等号．
综上可知：6m+3n的最小值是3+2
2
．
故答案为3+2
2
．
点评：熟练掌握重心定理和向量共线定理、向量运算法则等是解题的关键．
练习册系列答案
相关题目
（2013•蓟县二模）在正项等比数列{an}中，a2a4=4，S3=14，数列{bn}满足bn=log2an，则数列{bn}的前6项和是（　　）
（2013•蓟县二模）设f（x）=2x-2-x．若当θ∈[-
π
2
，0)时，f(m-
1
cosθ-1
)+f(m2-3)＞0恒成立，则实数m的取值范围是（　　）
（2013•蓟县二模）命题：“若 xy=0，则 x=0或 y=0”的逆否命题为：
若 x≠0且 y≠0 则 xy≠0
若 x≠0且 y≠0 则 xy≠0
．
（2013•蓟县二模）下列命题中，正确命题的个数为（　　）
①若xy=0，则x=0或y=0”的逆否命题为“若x≠0且y≠0，则xy≠0；
②函数f（x）=ex+x-2的零点所在区间是（1，2）；
③x=2是x2-5x+6=0的充分不必要条件．
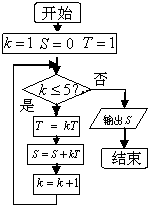（2013•蓟县二模）如果执行如面的程序框图，那么输出的S=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网