题目内容
已知函数f(x)=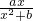 在x=1取得极值2,则当x>0时,函数
在x=1取得极值2,则当x>0时,函数
- A.有最小值2
- B.有最大值2
- C.有最小值4
- D.有最大值4
C
分析:由f(x)=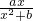 在x=1取得极值2这一条件,可求得f′(x),利用
在x=1取得极值2这一条件,可求得f′(x),利用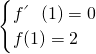 可求得a=4,b=1,
可求得a=4,b=1, =
= ,易知
,易知 .从而排除A,B,D,选C.
.从而排除A,B,D,选C.
解答:∵ ,
,
∴ 由题意得:
由题意得:
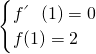 ,
,
∴a=4,b=1,
∴ ,
, ,
,
令y′≥0得x≥2或x≤-2(舍),令y′≤0得0<y≤2,
∴x=2时,y有最小值,y最小值=4.
故选C.
点评:本题考查导数的应用,解决的关键是对函数求导,得到a,b的方程组求得a,b的值,再对函数 .
.
分析:由f(x)=
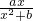 在x=1取得极值2这一条件,可求得f′(x),利用
在x=1取得极值2这一条件,可求得f′(x),利用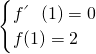 可求得a=4,b=1,
可求得a=4,b=1, =
= ,易知
,易知 .从而排除A,B,D,选C.
.从而排除A,B,D,选C.解答:∵
 ,
,∴
 由题意得:
由题意得: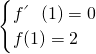 ,
,
∴a=4,b=1,
∴
 ,
, ,
,令y′≥0得x≥2或x≤-2(舍),令y′≤0得0<y≤2,
∴x=2时,y有最小值,y最小值=4.
故选C.
点评:本题考查导数的应用,解决的关键是对函数求导,得到a,b的方程组求得a,b的值,再对函数
 .
. 
练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目