题目内容
14.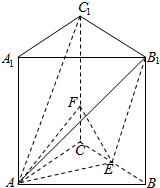 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=BC=AC=AA1=4,点F在CC1上,且C1F=3FC,E是BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=BC=AC=AA1=4,点F在CC1上,且C1F=3FC,E是BC的中点.(1)求证:AE⊥平面BCC1B1
(2)求四棱锥A-B1C1FE的体积;
(3)证明:B1E⊥AF.
分析 (1)易证AE⊥BC,BB1⊥AE,又BB1∩BC=B,BB1,BC?平面BB1C1C,即可证明AE⊥平面BB1C1C.
(2)由(1)知AE为四棱锥A-B1C1FE的高,由题意根据${S}_{四边形{B}_{1}{C}_{1}FE}$=${S}_{正方形B{B}_{1}{C}_{1}C}$-${S}_{△B{B}_{1}E}$-S△CFE即可得解.
(3)证明:连结B1F,由(1)可证AE⊥B1E,易求B1F,B1E,EF的值,由勾股定理可证B1E⊥EF,从而可证明B1E⊥平面AEF,根据AF?平面AEF,即可判定B1E⊥AF.
解答 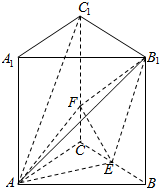 (本小题满分12分)
(本小题满分12分)
解:(1)∵AB=AC,E是BC的中点,
∴AE⊥BC.….(1分)
在三棱柱ABC-A1B1C1,中,BB1∥AA1,
∴BB1⊥平面ABC,
∵AE?平面ABC,
∴BB1⊥AE,….(2分)
又∵BB1∩BC=B,….(3分)
BB1,BC?平面BB1C1C,
∴AE⊥平面BB1C1C,….(4分)
(2)由(1)知,即AE为四棱锥A-B1C1FE的高,
在正三角形ABC中,AE=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$,…(5分)
在正方形BB1C1C,中,CE=BE=2,CF=1,
∴${S}_{四边形{B}_{1}{C}_{1}FE}$=${S}_{正方形B{B}_{1}{C}_{1}C}$-${S}_{△B{B}_{1}E}$-S△CFE=4×$4-\frac{1}{2}×2×4-\frac{1}{2}×2×1$=11.…(6分)
∴${V}_{A-{B}_{1}{C}_{1}FE}$=$\frac{1}{3}$${S}_{四边形{B}_{1}{C}_{1}FE}$•AE
=$\frac{1}{3}×11×2\sqrt{3}$
=$\frac{22\sqrt{3}}{3}$…(7分)
(3)证明:连结B1F,由(1)得AE⊥平面BB1C1C,
∵B1E?平面BB1C1C,∴AE⊥B1E,….(8分)
在正方形BB1C1C,中,B1F=$\sqrt{{B}_{1}{{C}_{1}}^{2}+{C}_{1}{F}^{2}}$=5,B1E=$\sqrt{B{E}^{2}+B{{B}_{1}}^{2}}$=2$\sqrt{5}$,
EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=$\sqrt{5}$,
∵B1F2=B1E2+EF2,
∴B1E⊥EF….(9分)
又∵AE∩EF=E,….(10分)
AE,EF?平面AEF,
∴B1E⊥平面AEF,….(11分)
∵AF?平面AEF,
∴B1E⊥AF.….(12分)
点评 本题主要考查了直线与平面垂直的性质,四棱锥体积的求法,直线与平面、平面与平面垂直的判定定理的应用,考查了空间想象能力和推理论证能力,属于中档题.

| A. | (-7,+∞) | B. | (-7,$\frac{1}{2}}$)∪(${\frac{1}{2}$,+∞) | C. | [-7,+∞) | D. | [-7,$\frac{1}{2}}$)∪(${\frac{1}{2}$,+∞) |
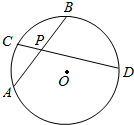 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )| A. | 7 | B. | $\sqrt{39}$ | C. | $\sqrt{7}$ | D. | 8 |
| A. | 总体容量越大,估计越精确 | B. | 总体容量越小,估计越精确 | ||
| C. | 样本容量越大,估计越精确 | D. | 样本容量越小,估计越精确 |
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求η的分布列及期望E(η).
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
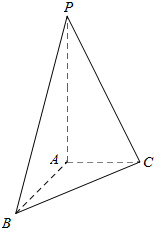 如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.
如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.