题目内容
 若函数f(x)=sinωxcosωx-
若函数f(x)=sinωxcosωx-| 3 |
| ||
| 2 |
(Ⅰ)求ω的值及f(x)的单调递增区间;
(Ⅱ)若f(x)的图象与f(x)的图象与关于点(-
| 1 |
| 3 |
考点:两角和与差的正弦函数,函数恒成立问题,正弦函数的单调性
专题:三角函数的图像与性质
分析:(Ⅰ)利用二倍角公式和两角和公式对函数解析式化简,利用周期公式求得ω,根据正弦函数的性质求得函数的单调增区间.
解答:
解:(Ⅰ)f(x)=sinωxcosωx-
sin2ωx+
=
sin2ωx+
cos2ωx
=sin(2ωx+
),
∴f(x)max=1,
=2,T=4,
由
=4,
∴ω=
∴f(x)=sin(
x+
),
其递增区间满足:-
+2kπ≤
x+
≤
+2kπ,k∈Z,
∴f(x)的单调递增区间为[4k-
,4k+
],k∈Z.
(Ⅱ)由已知g(x)=-f(-
-x)=-sin[
(-
-x)+
]=sin
x,
由 m2+[g(x)]2>4[m+g(-x)],得m2-4m>-[g(x)]2+4g(-x),
设t=-[g(x)]2+4g(-x)=sin2
x+4sin[
(-x)]=-sin2
x-4sin
x=-(sin
x+2)2+4,
∵x∈R,
∴sin
x=-1时,t有最大值,且tmax=-1+4=3,
∴m2-4m>3,即m2-4m-3>0,
解得m<2-
或m>2+
.
| 3 |
| ||
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2ωx+
| π |
| 3 |
∴f(x)max=1,
| T |
| 2 |
由
| T |
| 2ω |
∴ω=
| π |
| 4 |
∴f(x)=sin(
| π |
| 2 |
| π |
| 3 |
其递增区间满足:-
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴f(x)的单调递增区间为[4k-
| 5 |
| 3 |
| 1 |
| 3 |
(Ⅱ)由已知g(x)=-f(-
| 2 |
| 3 |
| π |
| 2 |
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
由 m2+[g(x)]2>4[m+g(-x)],得m2-4m>-[g(x)]2+4g(-x),
设t=-[g(x)]2+4g(-x)=sin2
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∵x∈R,
∴sin
| π |
| 2 |
∴m2-4m>3,即m2-4m-3>0,
解得m<2-
| 7 |
| 7 |
点评:本题主要考查了三角函数图象与性质,运用了函数的思想及转化与化归的思想.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
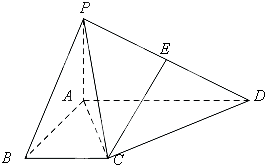 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2PA=2BC=2.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD=2PA=2BC=2.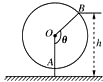 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转到θ角到OB,设B点与地面距离是h.