题目内容
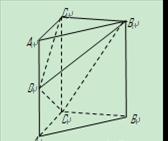
如图,在正三棱柱ABC—A1B1C1中,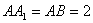 .
.
 (Ⅰ)求直线
(Ⅰ)求直线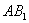 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅱ)在线段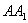 上是否存在点
上是否存在点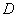 ?使得二面角
?使得二面角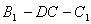 的大小为60°,若存在,求出
的大小为60°,若存在,求出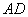 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
解:如图,以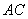 中点为原点建立空间直角坐标系,
中点为原点建立空间直角坐标系,
可得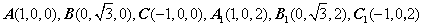 .
.
(Ⅰ)所以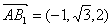 ,平面
,平面 的一个法向量
的一个法向量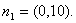
所以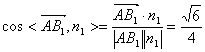 ,
,
 所以直线
所以直线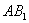 与平面
与平面 所成角的正弦值为
所成角的正弦值为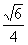 .
.
(Ⅱ)假设存在满足条件的点 ,设AD=
,设AD=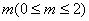 ,
,
则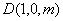 ,设平面
,设平面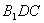 的法向量
的法向量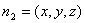 ,
,
因为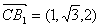 ,
,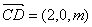 ,
,
且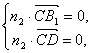
所以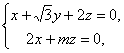
所以平面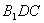 的一个法向量
的一个法向量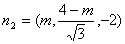
又因为平面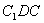 的一个法向量
的一个法向量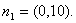
所以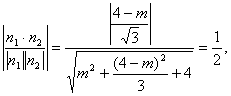
解得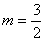 ,因为
,因为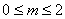 ,此时
,此时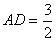 ,
,
所以存在点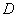 ,使得二面角B1—DC—C1的大小为60°.
,使得二面角B1—DC—C1的大小为60°.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 ,若
,若 时,
时, 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是 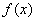 的导函数
的导函数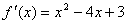 ,则
,则 的单调递减区间是 .
的单调递减区间是 .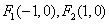 是椭圆的两个焦点,过
是椭圆的两个焦点,过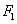 的直线
的直线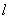 交椭圆于
交椭圆于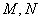 两点,若
两点,若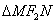 的周长为
的周长为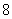 ,则椭圆方程为( )
,则椭圆方程为( )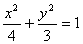 (B)
(B)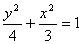
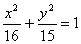 (D)
(D)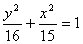
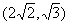 的双曲线
的双曲线 的渐近线方程为
的渐近线方程为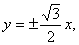
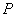 为双曲线
为双曲线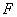 为双曲线
为双曲线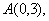 则
则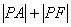 的最小值为 .
的最小值为 .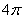 B.
B.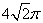 C.
C. D.
D.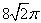
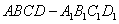 的外接球
的外接球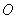 的体积为
的体积为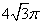 ,则球心
,则球心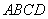 的距离为 ( )
的距离为 ( )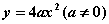 的焦点坐标为
的焦点坐标为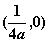 B、
B、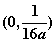 C、
C、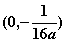 D、
D、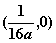
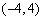 的抛物线的标准方程是 .
的抛物线的标准方程是 .