题目内容
如图,已知⊙O1与⊙O2相切于点P,过P的直线分别交⊙O1、⊙O2于A、B,过B作⊙O2的切线交⊙O1于点C、D,CP的延长线交⊙O2于点Q,求证: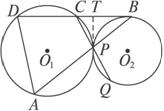
.
图19
证明:过P作两圆的公切线PT交BD于T点.
则∠CPT=∠CDP.
∵BD是⊙O2的切线,
∴∠B=∠BPT.
∵∠APD=∠CDP+∠B,∠BPC=∠BPT+∠CPT.
∴∠APD=∠BPC.又∵∠BCP=∠A,
∴△PAD∽△PCB.∴
.
∴.∵BC是⊙O2的切线,
∴BC2=PC·CQ.∴
.
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
（2012•许昌二模）如图，已知⊙O1与⊙O2外切于点P，AB是两圆的外公切线，A，B为切点，AB与O1O2的延长线相交于点C，延长AP交⊙O2于点D，点E在AD延长线上，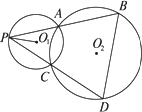
，求
的值。
，求
的值．
，求
的值．