题目内容
(选做题)
如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD的延长线上。
(Ⅰ)求证:△ABP是直角三角形;
(Ⅱ)若AB·AC=AP·AE,AP=4, ,求
,求 的值。
的值。
如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD的延长线上。
(Ⅰ)求证:△ABP是直角三角形;
(Ⅱ)若AB·AC=AP·AE,AP=4,
 ,求
,求 的值。
的值。
证明:(Ⅰ)过点P作两圆公切线PN交AB于N,
由切线长定理得 ,
,
∴△PAB为直角三角形;
(Ⅱ)∵ ,
,
∴ ,
,
又 ,
,
∴ ,
,
∴
即 ,
,
由切割线定理, ,
,
∴ ,
,
∴ 。
。
由切线长定理得
 ,
,∴△PAB为直角三角形;
(Ⅱ)∵
 ,
, ∴
 ,
,又
 ,
,∴
 ,
,∴

即
 ,
,由切割线定理,
 ,
, ∴
 ,
, ∴
 。
。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 15、(几何证明选做题)如图,已知:△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠B=30°,AC=2,则OD的长为
15、(几何证明选做题)如图,已知:△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠B=30°,AC=2,则OD的长为 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)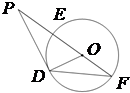 (2013•河西区一模)(几何证明选做题)如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
(2013•河西区一模)(几何证明选做题)如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4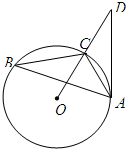 (2011•广州模拟)(几何证明选讲选做题)
(2011•广州模拟)(几何证明选讲选做题) (2008•深圳二模)(几何证明选讲选做题)如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,DF⊥EB于点F,若BC=6,AC=8,则DF=
(2008•深圳二模)(几何证明选讲选做题)如图,已知EB是半圆O的直径,A是BE延长线上一点,AC切半圆O于点D,BC⊥AC于C,DF⊥EB于点F,若BC=6,AC=8,则DF=