题目内容
如图，已知⊙O1与⊙O2交于A、C两点，P为⊙O1上任一点，连结PA、PC并延长，分别交⊙O2于B、D．
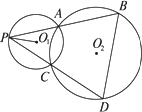
求证：O1P⊥BD．
答案：
解析：
解析：
|
证明：过P作⊙O1的切线PE，P为切点，连结AC，所以∠1＝∠2，O1P垂直于PE．
因为∠2＝∠B， 所以∠1＝∠B．因为PE平行于BD，所以O1P⊥BD． 分析：要证O1P⊥BD，我们知道O1P为⊙O1的半径，它与过P的切线是垂直的，故只需证过P点的⊙O1的切线与BD平行即可，注意：有半径(或直径)时，常过端点作此圆的切线． |
练习册系列答案
相关题目
（2012•许昌二模）如图，已知⊙O1与⊙O2外切于点P，AB是两圆的外公切线，A，B为切点，AB与O1O2的延长线相交于点C，延长AP交⊙O2于点D，点E在AD延长线上，
，求
的值。
，求
的值．
，求
的值．