题目内容
已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆C的标准方程；
（2）若过点F且斜率不为零的直线交椭圆与B、C两点，直线A1B、A1C分别交l于点M、N，试判断点F是否在以MN为直径的圆上．
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：（1）由准线方程和椭圆的性质，以及a，b，c的关系式，即可得到椭圆方程；
（2）设过点F且斜率不为零的直线BC：y=k（x-1），与椭圆方程联立，消去y，得到二次方程，运用韦达定理，设M（4，m），N（4，n），运用三点共线知识，再计算
•
是否为0，注意化简整理，即可判断．
（2）设过点F且斜率不为零的直线BC：y=k（x-1），与椭圆方程联立，消去y，得到二次方程，运用韦达定理，设M（4，m），N（4，n），运用三点共线知识，再计算
| MF |
| NF |
解答：
解：（1）由题意得，a-c=1，
=4，解得，a=2，c=1，由b2=a2-c2=3，
则椭圆C的标准方程为：
+
=1．
（2）设过点F且斜率不为零的直线BC：y=k（x-1），
与椭圆方程联立，消去y，得到（3+4k2）x2-8k2x+4k2-12=0，
设B（x1，y1），C（x2，y2），则x1+x2=
，x1x2=
，
设M（4，m），N（4，n），则
=（-3，-m），
=（-3，-n），
由A1，B，M共线，得
=
，
由A1，C，N共线，得
=
．
则
•
=9+mn=9+
=9+36•k2•
=9+36k2•
=0，
故
⊥
，即有点F在以MN为直径的圆上．
| a2 |
| c |
则椭圆C的标准方程为：
| x2 |
| 4 |
| y2 |
| 3 |
（2）设过点F且斜率不为零的直线BC：y=k（x-1），
与椭圆方程联立，消去y，得到（3+4k2）x2-8k2x+4k2-12=0，
设B（x1，y1），C（x2，y2），则x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
设M（4，m），N（4，n），则
| MF |
| NF |
由A1，B，M共线，得
| y1 |
| x1+2 |
| m |
| 6 |
由A1，C，N共线，得
| y2 |
| x2+2 |
| n |
| 6 |
则
| MF |
| NF |
| 36y1y2 |
| (x1+2)(x2+2) |
| (x1-1)(x2-1) |
| (x1+2)(x2+2) |
=9+36k2•
| (4k2-12)+(3+4k2)-8k2 |
| (4k2-12)+4(3+4k2)+16k2 |
故
| MF |
| NF |
点评：本题考查椭圆的方程和性质，主要是准线方程，考查直线方程和椭圆方程联立，消去一个未知数，运用韦达定理，同时考查向量的垂直的条件，属于中档题．
练习册系列答案
相关题目
若P、Q是两个非空数集，定义P与Q的差集P-Q={x|x∈P且x∉Q}，已知集合A={x|a＜x＜0}，集合B={x|-b＜x＜b}，其中a，b是满足|a|≥|b|的整数，在集合A中随机取一个整数c，若c属于差集A-B的概率P1=
，属于集合A∩B的概率P2=
，则整数a，b应满足的条件是（ ）
| 2 |
| 3 |
| 1 |
| 3 |
| A、a+3b=-1（b≥1，b∈Z） |
| B、a+3b=-1，（b≥2，b∈Z） |
| C、a+3b=2（b≥1，b∈Z） |
| D、a+3b=2，（b≥2，b∈Z） |
设
，
是两个非零向量，则下列命题正确的是（ ）
| a |
| b |
A、若
| ||||||||||||
B、若|
| ||||||||||||
C、若存在实数λ，使得
| ||||||||||||
D、若|
|
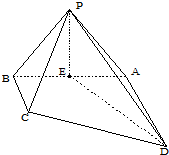如图，四棱锥P-ABCD中，底面ABCD是直角梯形，∠DAB=90°，AD∥BC，AD⊥侧面PAB，△PAB是等边三角形，DA=AB=2=0，BC=