题目内容
(本小题满分12分)如图所示,在长方体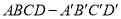 中,
中,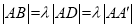 ,(
,(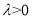 ),
),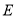 、
、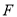 分别是
分别是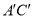 和
和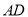 的中点,且
的中点,且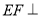 平面
平面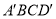 .
.

(1)求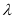 的值;
的值;
(2)求二面角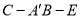 的余弦值.
的余弦值.
(1)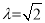 ;(2)
;(2)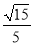 .
.
【解析】
试题分析:(1)分析题意,以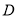 为原点,
为原点,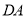 ,
,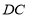 ,
,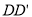 的方向分别作为
的方向分别作为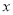 ,
,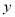 ,
,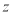 轴的正方向建立空间直角坐标系,分别求出
轴的正方向建立空间直角坐标系,分别求出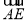 ,
,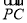 的坐标,计算向量的数量积,求得
的坐标,计算向量的数量积,求得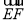 ,
,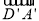 ,
,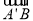 ,则由条件可知
,则由条件可知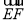 是平面
是平面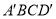 的法向量,利用
的法向量,利用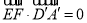 ,
,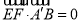 即可求得
即可求得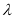 的值;(2)分别求出平面
的值;(2)分别求出平面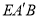 与平面
与平面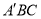 的一个法向量,利用法向量即可求得二面角
的一个法向量,利用法向量即可求得二面角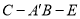 的余弦值.
的余弦值.
试题解析:以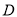 为原点,
为原点,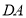 ,
,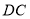 ,
,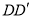 为
为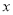 ,
,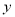 ,
, 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设 ,则
,则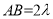 ,则
,则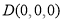 ,
, ,
,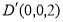 ,
,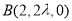 ,
,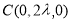 ,
,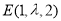 ,
,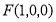 , 2分
, 2分
(1)由已知可得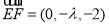 ,
,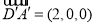 ,
,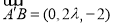 , 3分
, 3分
∵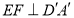 ,
,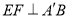 ,∴
,∴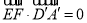 ,
,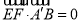 , 4分
, 4分
即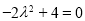 ,∴
,∴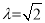 ; 5分
; 5分
(2)设平面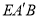 的法向量为
的法向量为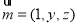 ,则
,则 ,
,
∵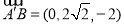 ,
, ,∴
,∴ ,∴
,∴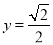 ,
,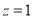 ,
,
∴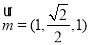 , 7分
, 7分
由(1)可得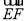 为平面
为平面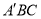 的法向量,且
的法向量,且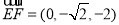 , 9分
, 9分
∴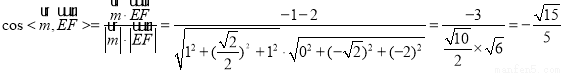 , 11分
, 11分
又∵二面角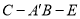 为锐二面角,∴二面角
为锐二面角,∴二面角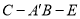 的余弦值为
的余弦值为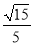 . 12分
. 12分
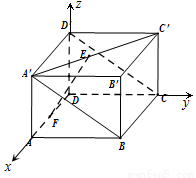
考点:1.线面垂直的性质;2.空间向量的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分12分)
某网站针对“2015年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如下表(单位:万人):
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 |
|
已知从所有参与调查的人中任选1人是“老年人”的概率为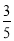 .
.
(Ⅰ)求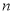 的值;
的值;
(Ⅱ)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.
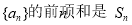 ,且
,且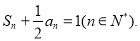
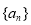 的通项公式;
的通项公式;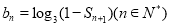 ,求适合方程
,求适合方程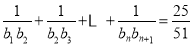 的正整数
的正整数 的值。
的值。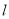 的参数方程为
的参数方程为 (
(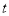 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,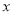 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程是
的极坐标方程是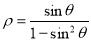 .
. 的极坐标方程与曲线
的极坐标方程与曲线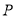 是曲线
是曲线 距离的最小值,并求出此时
距离的最小值,并求出此时 上任取一个数
上任取一个数 ,则使得
,则使得 的概率为( )
的概率为( ) B.
B. C.
C. D.
D.
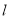 的参数方程为
的参数方程为 (
(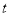 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,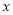 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线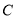 的极坐标方程是
的极坐标方程是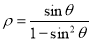 .
.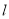 的极坐标方程与曲线
的极坐标方程与曲线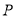 是曲线
是曲线 距离的最小值,并求出此时
距离的最小值,并求出此时 的展开式中
的展开式中 的系数为______.(用数字作答)
的系数为______.(用数字作答)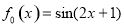 ,若输出的
,若输出的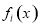 是
是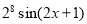 ,则程序框图中的判断框应填入( )
,则程序框图中的判断框应填入( )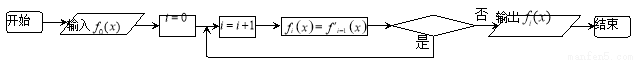
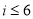 B.
B. C.
C.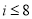 D.
D.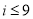
 ,点
,点 ,使得
,使得 的概率为 .
的概率为 .