题目内容
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线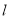 的参数方程为
的参数方程为 (
(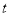 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,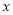 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线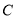 的极坐标方程是
的极坐标方程是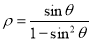 .
.
(1)写出直线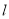 的极坐标方程与曲线
的极坐标方程与曲线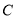 的普通方程;
的普通方程;
(2)若点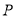 是曲线
是曲线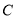 上的动点,求
上的动点,求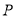 到直线
到直线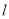 距离的最小值,并求出此时
距离的最小值,并求出此时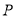 点的坐标.
点的坐标.
(1)极坐标方程: ,普通方程:
,普通方程: ;
;
(2)当 点为
点为 时,
时, 到直线
到直线 的距离最小,最小值为
的距离最小,最小值为 .
.
【解析】
试题分析:(1)可以先消参数,求出直线 的普通方程,再利用公式将曲线
的普通方程,再利用公式将曲线 的极坐标方程化为平面直角坐标方程;
的极坐标方程化为平面直角坐标方程;
(2)利用点到直线的距离公式,求出 到直线
到直线 的距离的最小值,再根据函数取最值的情况求出
的距离的最小值,再根据函数取最值的情况求出 点的坐标,得到本题结论.
点的坐标,得到本题结论.
试题解析:(1)由 ,得
,得 , 1分
, 1分
∴直线 的极坐标方程为:
的极坐标方程为: ,
,
即 ,即
,即 , 3分
, 3分
∵ ,∴
,∴ ,∴
,∴ ,∴
,∴ ,
,
即曲线 的普通方程为
的普通方程为 ; 5分
; 5分
(2)设 ,
, ,
,
∴ 到直线
到直线 的距离
的距离 , 8分
, 8分
∴当 时,
时, ,∴此时
,∴此时 ,
,
∴当 点为
点为 时,
时, 到直线
到直线 的距离最小,最小值为
的距离最小,最小值为 . 10分
. 10分
考点:1.参数方程化为普通方程;2.简单曲线的极坐标方程.

练习册系列答案
相关题目
 满足:
满足: ,则数列
,则数列 的整数
的整数 ,输出的数列的通项公式是 ( )
,输出的数列的通项公式是 ( )
 B.
B.
 D.
D.
 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点,交抛物线的准线于
两点,交抛物线的准线于 ,若
,若 ,
, ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.3
D.3 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
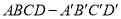 中,
中,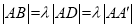 ,(
,(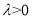 ),
),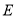 、
、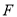 分别是
分别是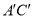 和
和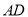 的中点,且
的中点,且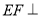 平面
平面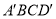 .
.
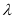 的值;
的值;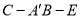 的余弦值.
的余弦值. 截球
截球 的球面得圆
的球面得圆 ,过圆心
,过圆心 与
与 ,且平面
,且平面 ,已知球
,已知球 ,则圆
,则圆 C.4 D.
C.4 D.
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.