题目内容
已知向量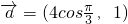
，
，
．
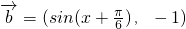（1）求f（x）的单调增区间；
（2）求f（x）在区间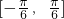
上的最大值和最小值．
解：（1）
．…2′
由
得：
，（k∈z）．
∴f（x）的单调增区间是
（k∈z）．…6′
（2）由（1）知f（x）在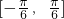上递增，∴当
时，f（x）取得最小值-1；
当
时，f（x）取得最大值
．…12′
分析：（1）利用两个向量的数量积公式化简函数f（x）的解析式为sin（x+
）-1，由求得x的范围，即可求得f（x）的单调增区间．
（2）由（1）知f（x）在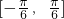上递增，由此求得f（x）在区间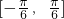上的最大值和最小值．
点评：本题主要考查两个向量的数量积公式的应用，正弦函数的定义域和值域以及单调性，属于中档题．
．…2′由
得：，（k∈z）．∴f（x）的单调增区间是
（k∈z）．…6′（2）由（1）知f（x）在
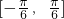上递增，∴当时，f（x）取得最小值-1；当
时，f（x）取得最大值．…12′分析：（1）利用两个向量的数量积公式化简函数f（x）的解析式为sin（x+
）-1，由求得x的范围，即可求得f（x）的单调增区间．（2）由（1）知f（x）在
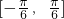上递增，由此求得f（x）在区间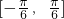上的最大值和最小值．点评：本题主要考查两个向量的数量积公式的应用，正弦函数的定义域和值域以及单调性，属于中档题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目