题目内容
从某校随机抽取20个班，调查各班中有网上购物经历的人数，所得数据的茎叶图和频率分布直方图如图．
（1）求频率分布直方图中m的值；
（2）若要从有网上购物经历的人数在区间[30，40]内的班级中任取两个班，求其中至少有一个班有网上购物经历的人数大于36的概率．
（1）求频率分布直方图中m的值；
（2）若要从有网上购物经历的人数在区间[30，40]内的班级中任取两个班，求其中至少有一个班有网上购物经历的人数大于36的概率．
考点：频率分布直方图,古典概型及其概率计算公式
专题：图表型,概率与统计
分析：（1）由茎叶图可知，第三组的频数为4，求出此组的频率，用频率÷组距得到m．
（2）由茎叶图可知，有网上购物经历的人数在区间[30，40]内的班级共有5个，通过列举法得到任取两个班级的方法数及至少有一个办有网上购物经历的方法数，利用古典概型的概率公式求出概率．
（2）由茎叶图可知，有网上购物经历的人数在区间[30，40]内的班级共有5个，通过列举法得到任取两个班级的方法数及至少有一个办有网上购物经历的方法数，利用古典概型的概率公式求出概率．
解答：
（本小题12分）
解：（1）由茎叶图可知，第三组的频数为4，频率为
=0.2，…（3分）
则m=
=0.04…（6分）
（2）记事件Q：至少有一个班有网上购物经历的人数大于36．
由茎叶图可知，有网上购物经历的人数在区间[30，40]内的班级共有5个，不妨设为A，B，C，D，E，其中有网上购物经历的人数大于36的2个班级为A，B．
则从A，B，C，D，E中任取2个，有AB，AC，AD，AE，BC，BD，BE，CD，CE，DE共10种，…（8分）
其中A，B至少有一个的有AB，AC，AD，AE，BC，BD，BE共7种，…（10分）
所以p(Q)=
=0.7．…（12分）
解：（1）由茎叶图可知，第三组的频数为4，频率为
| 4 |
| 20 |
则m=
| 0.2 |
| 5 |
（2）记事件Q：至少有一个班有网上购物经历的人数大于36．
由茎叶图可知，有网上购物经历的人数在区间[30，40]内的班级共有5个，不妨设为A，B，C，D，E，其中有网上购物经历的人数大于36的2个班级为A，B．
则从A，B，C，D，E中任取2个，有AB，AC，AD，AE，BC，BD，BE，CD，CE，DE共10种，…（8分）
其中A，B至少有一个的有AB，AC，AD，AE，BC，BD，BE共7种，…（10分）
所以p(Q)=
| 7 |
| 10 |
点评：（1）本题考查茎叶图及频率分布直方图，古典概型的概率公式，属于一道基础题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若平面内两个向量
=（2cosθ，1）与
=（1，cosθ）共线，则cos2θ等于（ ）
| a |
| b |
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
如图是甲，乙两名同学5次综合测评成绩的茎叶图，下列四个结论中，正确的是（ ）
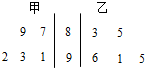
| A、甲成绩的极差大于乙成绩的极差 |
| B、甲成绩的中位数小于乙成绩的中位数 |
| C、甲成绩的平均值等于乙成绩的平均值 |
| D、甲成绩的标准差小于乙成绩的标准差 |
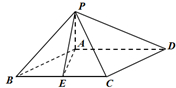如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠ABC=60°，又PA⊥底面ABCD，AB=2PA，E为BC的中点．
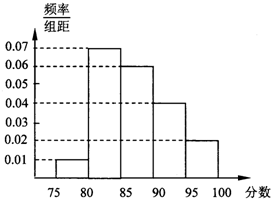某市教育局为了了解高三学生体育达标情况，在某学校的高三学生体育达标成绩中随机抽取100个进行调研，按成绩分组：第l组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]得到的频率分布直方图如图所示：若要在成绩较高的第3，4，5组中用分层抽样抽取6名学生进行复查：