题目内容
若方程 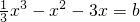 有3个不同实数解,则b的取值范围为________.
有3个不同实数解,则b的取值范围为________.

分析:构造f(x)=
 ,通过函数的导数求出函数的极值,然后利用三个不等实根,可得b的取值范围.
,通过函数的导数求出函数的极值,然后利用三个不等实根,可得b的取值范围.解答:假设f(x)=
 ,则f′(x)=x2-2x-3=(x+1)(x-3)
,则f′(x)=x2-2x-3=(x+1)(x-3)∴函数在(-∞,-1),(3,+∞)上单调增,在(-1,3)上单调减
∴f(-1)=
 为极大值,f(3)=-9为极小值
为极大值,f(3)=-9为极小值所以即-9<b<
 时,函数f(x)=
时,函数f(x)= 与函数f(x)=b有三个交点,方程有3个不等实根
与函数f(x)=b有三个交点,方程有3个不等实根故答案为:
 .
.点评:本题以方程为载体,考查方程根问题,考查函数与方程的联系,解题的关键是构造函数,利用导数求函数的极值.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目

 的单调区间和极值;
的单调区间和极值; 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围. 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. .
. 的极值点;
的极值点; 的方程
的方程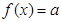 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.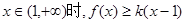 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 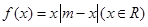 ,且
,且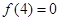 ,若关于
,若关于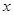 的方程
的方程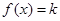 有3个不同实根,则实数k的取值范围是( )
有3个不同实根,则实数k的取值范围是( )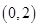 B.
B. 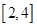 C.
C.  D.
D. 
 若关于
若关于 的方程
的方程 有3个不同实根,则实数a的取值范围
有3个不同实根,则实数a的取值范围