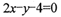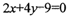题目内容
已知抛物线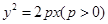 ,当过
,当过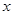 轴上一点
轴上一点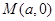 的直线
的直线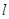 与抛物线交于
与抛物线交于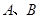 两点时,
两点时,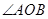 为锐角,则
为锐角,则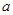 的取值范围 ( )
的取值范围 ( )
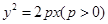 ,当过
,当过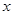 轴上一点
轴上一点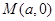 的直线
的直线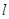 与抛物线交于
与抛物线交于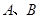 两点时,
两点时,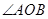 为锐角,则
为锐角,则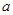 的取值范围 ( )
的取值范围 ( )A.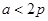 | B.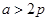 | C.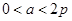 | D.以上选项都不对 |
D
当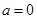 时,显然成立;
时,显然成立;
当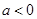 时,直线
时,直线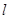 斜率存在,设直线
斜率存在,设直线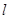 方程为
方程为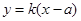 ,联立
,联立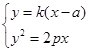 可得
可得 。设
。设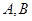 坐标分别为
坐标分别为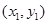 ,
,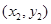 ,则
,则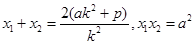 ,从而可得
,从而可得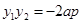 。因为
。因为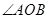 为锐角,所以
为锐角,所以 。因为
。因为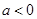 ,所以
,所以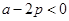 ,解得
,解得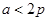 。所以此时
。所以此时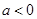 ;
;
当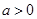 时,若直线
时,若直线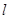 斜率不存在,则此时直线
斜率不存在,则此时直线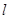 方程为
方程为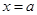 ,可得
,可得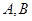 坐标为
坐标为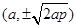 ,
,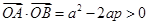 。因为
。因为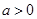 ,所以
,所以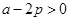 ,解得
,解得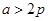 。若直线
。若直线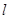 斜率存在,设直线
斜率存在,设直线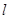 方程为
方程为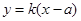 ,联立
,联立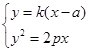 可得
可得 。设
。设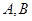 坐标分别为
坐标分别为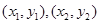 ,则
,则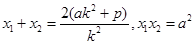 ,从而可得
,从而可得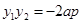 。因为
。因为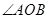 为锐角,所以
为锐角,所以 。同理可得,
。同理可得,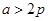 。所以此时
。所以此时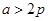 。
。
综上可得,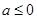 或
或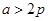 ,故选D
,故选D
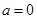 时,显然成立;
时,显然成立;当
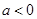 时,直线
时,直线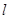 斜率存在,设直线
斜率存在,设直线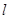 方程为
方程为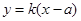 ,联立
,联立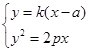 可得
可得 。设
。设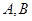 坐标分别为
坐标分别为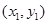 ,
,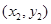 ,则
,则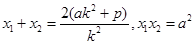 ,从而可得
,从而可得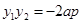 。因为
。因为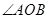 为锐角,所以
为锐角,所以 。因为
。因为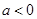 ,所以
,所以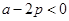 ,解得
,解得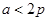 。所以此时
。所以此时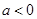 ;
;当
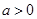 时,若直线
时,若直线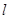 斜率不存在,则此时直线
斜率不存在,则此时直线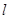 方程为
方程为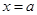 ,可得
,可得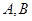 坐标为
坐标为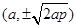 ,
,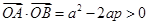 。因为
。因为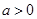 ,所以
,所以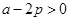 ,解得
,解得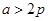 。若直线
。若直线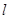 斜率存在,设直线
斜率存在,设直线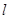 方程为
方程为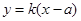 ,联立
,联立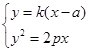 可得
可得 。设
。设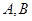 坐标分别为
坐标分别为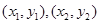 ,则
,则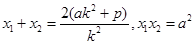 ,从而可得
,从而可得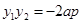 。因为
。因为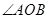 为锐角,所以
为锐角,所以 。同理可得,
。同理可得,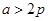 。所以此时
。所以此时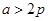 。
。综上可得,
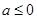 或
或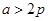 ,故选D
,故选D
练习册系列答案
相关题目
 2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则
2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则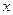 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐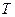 ,过点
,过点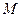 ,过点
,过点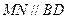 ,交线段
,交线段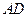 于点
于点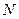 ,连接
,连接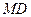 ,使
,使 ~
~ ,若存在,求出点
,若存在,求出点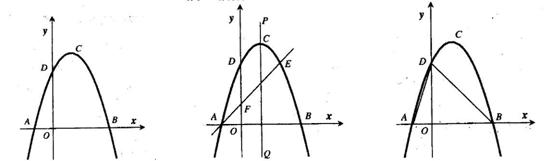 图1 图2
图1 图2  图3
图3 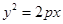 的通径是
的通径是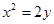 上距离点A
上距离点A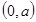 的最近点恰好是抛物线的顶点,则
的最近点恰好是抛物线的顶点,则 的取值范围是( )
的取值范围是( )
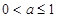
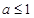


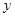 =4
=4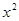 的焦点坐标是( )
的焦点坐标是( )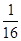 )
)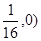
 上纵坐标为
上纵坐标为 的点
的点 到焦点的距离为2.
到焦点的距离为2.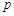 的值;
的值;

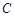 为抛物线上三点,且线段
为抛物线上三点,且线段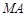 ,
, ,
,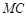 与
与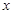 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若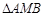 的面积是
的面积是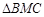 面积的
面积的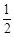 ,求直线
,求直线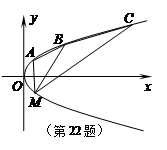
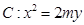
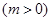 和直线
和直线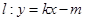 没有公共点(其中
没有公共点(其中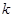 、
、 为常数),动点
为常数),动点 是直线
是直线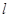 上的任意一点,过
上的任意一点,过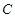 的两条切线,切点分别为
的两条切线,切点分别为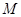 、
、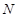 ,且直线
,且直线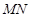 恒过点
恒过点 .
.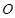 点为原点,连结
点为原点,连结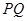 交抛物线
交抛物线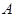 、
、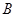 两点,
两点,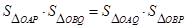 .
.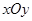 中,点P是曲线C上任意一点,点P到两点
中,点P是曲线C上任意一点,点P到两点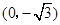 ,
,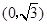 的距离之和等于4,直线
的距离之和等于4,直线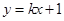 与C交于A,B两点.
与C交于A,B两点.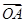
 ,求k的值。
,求k的值。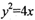 交于A,B两点;线段AB中点为
交于A,B两点;线段AB中点为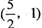 ,则直线l的方程为
,则直线l的方程为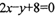
 、
、