题目内容

若二次函数f （x）=ax2+bx+c（a≠0）的部分对应值如下所示：
x -2 1 3
f （x） 0 -6 0
则不等式f （x）＜0的解集为（　　）
A．（-2，3）B．（-∞，-2）∪（3，+∞）C．（-2，1）D．（1，3）
由于函数过点（-2，0），（3，0）
则y=ax2+bx+c=a（x+2）（x-3），
又由函数f （x）过点（1，-6）
则a（1+2）（1-3）=-6，解得a=1
故y=（x+2）（x-3）
则f（x）＜0的解集是：（-2，3）．
故答案为 A
练习册系列答案
相关题目
若二次函数f（x）=ax2-4x+c的值域为[0，+∞），则
a
c2+4
+
c
a2+4
的最小值为
 
．
若二次函数f（x）=x2+bx+c满足f（2）=f（-2），且函数的f（x）的一个零点为1．
（Ⅰ） 求函数f（x）的解析式；
（Ⅱ）对任意的x∈[
12
，+∞)，4m2f（x）+f（x-1）≥4-4m2恒成立，求实数m的取值范围．
若二次函数f （x）=ax2+bx+c（a≠0）的部分对应值如下所示：
x -2 1 3
f （x） 0 -6 0
则不等式f （x）＜0的解集为（　　）
若二次函数f（x）=ax2+bx+1（a，b为实数且x∈R）．
（1）若函数f（x）为偶函数，且满足f（x）=2x有两个相等实根，求a，b的值；
（2）若f（-1）=0，且函数f（x）的值域为[0，+∞），求函数f（x）的表达式；
（3）在（2）的条件下，当x∈[-2，2]时，g（x）=f（x）-kx是单调函数，求实数k的取值范围．
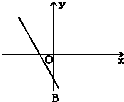精英家教网若二次函数f（x）=ax2+bx的导函数f′（x）的图象如图所示，则二次函数f（x）的顶点在（　　）
A、第四象限B、第三象限C、第二象限D、第一象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网