题目内容
若二次函数f(x)=x2+bx+c满足f(2)=f(-2),且函数的f(x)的一个零点为1.
(Ⅰ) 求函数f(x)的解析式;
(Ⅱ)对任意的x∈[
,+∞),4m2f(x)+f(x-1)≥4-4m2恒成立,求实数m的取值范围.
(Ⅰ) 求函数f(x)的解析式;
(Ⅱ)对任意的x∈[
| 1 | 2 |
分析:(Ⅰ)由题意可得函数图象的对称轴为x=0,求得b=0,再由f(1)=0求得c=-1,从而得到函数的解析式.
(Ⅱ)由题意知,得m2≥
+
-
在[
,+∞)上恒成立.令g(x)=
+
-
,求得g(x)的最大值
,从而得到m2≥
,由此求得实数m的取值范围.
(Ⅱ)由题意知,得m2≥
| 1 |
| x2 |
| 1 |
| 2x |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| x2 |
| 1 |
| 2x |
| 1 |
| 4 |
| 19 |
| 4 |
| 19 |
| 4 |
解答:解:(Ⅰ)∵f(2)=f(-2)且f(1)=0,故函数图象的对称轴为x=0,
∴b=0,c=-1,∴f(x)=x2-1.…(4分)
(Ⅱ)由题意知:4m2(x2-1)+(x-1)2-1+4m2-4≥0,在x∈[
,+∞)上恒成立,
整理得m2≥
+
-
在[
,+∞)上恒成立.…(6分)
令g(x)=
+
-
=(
+
)2-
,
∵x∈[
,+∞),∴
∈(0,2],…(8分)
当
=2时,函数g(x)的最大值
,…(10分)
所以m2≥
,解得m≤-
或m≥
. …(12分)
∴b=0,c=-1,∴f(x)=x2-1.…(4分)
(Ⅱ)由题意知:4m2(x2-1)+(x-1)2-1+4m2-4≥0,在x∈[
| 1 |
| 2 |
整理得m2≥
| 1 |
| x2 |
| 1 |
| 2x |
| 1 |
| 4 |
| 1 |
| 2 |
令g(x)=
| 1 |
| x2 |
| 1 |
| 2x |
| 1 |
| 4 |
| 1 |
| x |
| 1 |
| 4 |
| 5 |
| 16 |
∵x∈[
| 1 |
| 2 |
| 1 |
| x |
当
| 1 |
| x |
| 19 |
| 4 |
所以m2≥
| 19 |
| 4 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查二次函数的性质,函数的恒成立问题,求二次函数在闭区间上的最值,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
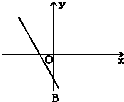 若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )
若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )| A、第四象限 | B、第三象限 | C、第二象限 | D、第一象限 |