题目内容
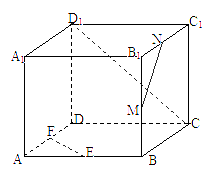
已知M、N、E、F分别是正方体ABCD—A1B1C1D1 的棱BB1、B1C1、AB和AD的中点.
(I)求异面直线MN和CD1所成的角;
(II)证明:EF//平面B1CD1.
(1)60°
解析:
(I)连结BC1、AD1、AC,则在正方体ABCD—A1B1C1D1中,AB、A1B1、C1D1
所以四边形ABC1D1为平行四边形,从而AD1//BC1.
又M、N分别为BB1,B1C1的中点,![]() ,进而MN//AD1.
,进而MN//AD1.
从而∠AD1C为异面直线MN与CD1所成的角. ………………4分
令正方体棱长为a,则AD1=D1C=AC=![]() . 即△AD1C为正三角形
. 即△AD1C为正三角形
所以![]() ,即异面直线MN和CD1所成的角为60° ……6分
,即异面直线MN和CD1所成的角为60° ……6分
(II)证明: ∵ BB1 //DD1 BB1 =DD1 ∴四边形BB1D1D是平行四边形
∴ BD // B1D1 ……8分
又E、F分别是棱、AB和AD的中点. ∴EF//BD ∴ EF // B1D1 ……10分
EF![]() 平面B1CD1 B1D1
平面B1CD1 B1D1![]() 平面B1CD1
平面B1CD1
∴EF//平面B1CD1 ……12分

练习册系列答案
相关题目
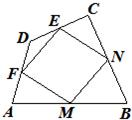 如图,已知:在四边形ABCD中,M、N、E、F分别是边AB、BC、CD、DA的中点.求证:四边形MNEF是平行四边形.
如图,已知:在四边形ABCD中,M、N、E、F分别是边AB、BC、CD、DA的中点.求证:四边形MNEF是平行四边形.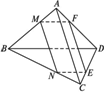

 如图,已知:在四边形ABCD中,M、N、E、F分别是边AB、BC、CD、DA的中点.求证:四边形MNEF是平行四边形.
如图,已知:在四边形ABCD中,M、N、E、F分别是边AB、BC、CD、DA的中点.求证:四边形MNEF是平行四边形.