题目内容
如图,已知M、N分别是□ABCD的边AB、边CD的中点,CM交BD于点E,AN交BD于点F,请你探讨BE、EF、FD三条线段之间的关系,并给出证明.

答案:
解析:
提示:
解析:
|
证明:因为四边形ABCD是平行四边形, M、N分别是边AB、CD的中点, 所以四边形AMCN是平行四边形(一组对边平行且相等的四边形一定是平行四边形). 因为在△CDE中,N是CD的中点,且FN平行于CE, 所以F是DE的中点,即DF=EF. 同理在△ABF中,M是AB的中点,且AF平行于ME, 所以E是BF的中点,即EF=BE. 所以BE=EF=DF. 分析:在△CDE中,N是边CD的中点,只要证明CE平行于FN,即可由推论1得DF等于EF,同理在△ABF中,根据M是边AB的中点,同样只要证明AF平行于ME,由推论1得EF=EB,由此可得BE、EF、FD三条线段之间的关系是BE=EF=FD. |
提示:
|
本题两次利用了M、N是中点的条件,在利用平行线等分线段定理或推论时要把平行和中点两个条件摆齐. |

练习册系列答案
相关题目
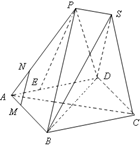 已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、
已知四边形ABCD为菱形,AB=6,∠BAD=60°,两个正三棱锥P-ABD、S-BCD(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,如图,E、M、N分别在AD、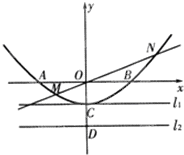 如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线
如图,已知抛物线与坐标轴分别交于A(-2,0)、B(2,0)、C(0,-1)三点,过坐标原点O的直线y=kx与抛物线交于M、N两点.分别过点C、D(0,-2)、作平行于x轴的直线 如图,已知A1,A2分别为椭圆
如图,已知A1,A2分别为椭圆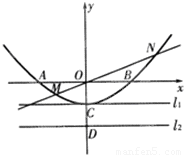
 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式; 表示),并证明M、N两
表示),并证明M、N两