题目内容
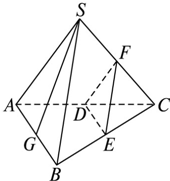 在三棱锥S-ABC中,D、E、F分别是AC、BC、SC的中点,G是AB上任意一点.
在三棱锥S-ABC中,D、E、F分别是AC、BC、SC的中点,G是AB上任意一点.(1)求证:SG∥平面DEF;
(2)如果三棱锥S-ABC中各条棱长均为a,G是AB的中点,求SG与平面ABC所成角的余弦值.
分析:(1)利用三角形中位线的性质,证明DE∥AB,利用线面平行的判定定理证明AB∥平面DEF,同理SA∥平面DEF,利用面面平行的判定定理,证明SG∥平面DEF;
(2)证明∠SGO 就是SG与平面ABC所成角,从而可求SG与平面ABC所成角的余弦值.
(2)证明∠SGO 就是SG与平面ABC所成角,从而可求SG与平面ABC所成角的余弦值.
解答:(1)证明:∵D、E分别是AC、BC的中点,
∴DE∥AB,
∵AB?平面DEF,DE?平面DEF,
∴AB∥平面DEF,
同理SA∥平面DEF,
∵AB∩SA=A,
∴平面SAB∥平面DEF,
⇒SG∥面DEF;
(2)解:∵SG=
a,S在面ABC内的射影O在CG上,且GO=
a
∴∠SGO 就是SG与平面ABC所成角,
∴cos∠SGO=
.
∴DE∥AB,
∵AB?平面DEF,DE?平面DEF,
∴AB∥平面DEF,
同理SA∥平面DEF,
∵AB∩SA=A,
∴平面SAB∥平面DEF,
|
(2)解:∵SG=
| ||
| 2 |
| ||
| 6 |
∴∠SGO 就是SG与平面ABC所成角,
∴cos∠SGO=
| 1 |
| 3 |
点评:本题考查线面平行,考查面面平行,考查线面角,正确运用线面平行,面面平行的判定定理是关键.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.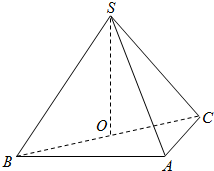 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,