题目内容
将参加夏令营的600名学生编号为：001，002，…，600，采用系统抽样的方法抽取一个容量为50的样本，且随机抽得的编号为003．这600名学生分住在3个营区，从001到300住在第1营区，从301到495住在第2营区，从496到600住在第3营区，则3个营区被抽中的人数依次为（ ）
| A、26，16，8 |
| B、25，16，9 |
| C、25，17，8 |
| D、24，17，9 |
考点：系统抽样方法
专题：概率与统计
分析：根据系统抽样的方法的要求，确定抽取间隔即可得到结论．
解答：
解：由题意知，被抽中的学生的编号满足y=12n-9（1≤n≤50，n∈N*）．
令1≤12n-9≤300，得1≤n≤25，
故第1营区被抽中的人数为25；
令301≤12n-9≤495，得26≤n≤42，
故第2营区被抽中的人数为17；
令496≤12n-9≤600得43≤n≤50，
故第3营区被抽中的人数为8．
故选：C
令1≤12n-9≤300，得1≤n≤25，
故第1营区被抽中的人数为25；
令301≤12n-9≤495，得26≤n≤42，
故第2营区被抽中的人数为17；
令496≤12n-9≤600得43≤n≤50，
故第3营区被抽中的人数为8．
故选：C
点评：本题主要考查系统抽样方法．根据系统抽样的定义确定抽取间距，利用等差数列的通项公式进行求解是解决本题的关键．
练习册系列答案
相关题目
已知直线kx-y=k-1与直线ky-x=2k，若0＜k＜
，则它们的交点在（ ）
| 1 |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
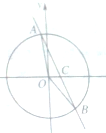如图所示，在平面坐标系中，直线y=-2x+b（0＜b＜1）与单位圆x2+y2=1相交于A，B（A在第二象限）两个不同的点，且∠AOB=α，∠BOC=β，则cos（α-2β）的值是（ ）A、-
| ||
B、
| ||
C、-
| ||
D、
|
在等差数列{an}中，若5a9-a13=60，则a4+a5+a8+a11+a12的值为（ ）
| A、70 | B、75 | C、80 | D、85 |
已知等差数列{an}，且a4+a8=2，则a6（a2+2a6+a10）的值为（ ）
| A、4 | B、6 | C、8 | D、10 |
设a=20.3，b=log
3，c=ln（ln2）则（ ）
| 2 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞a＞c |
| D、b＞c＞a |
设集合A={x|-1＜x＜3}，集合B={x|x≥1}，则A∩B=（ ）
| A、{x|1＜x＜3} |
| B、{x|1≤x＜3} |
| C、{x|1＜x≤3} |
| D、{x|1≤x≤3} |