题目内容
已知圆C1:x2-2x+y2=1,圆C2:x2-4x+y2=0,则圆C1与圆C2相交的弦长为
.
| 7 |
| 7 |
分析:把圆的方程化为标准形式,求得圆心和半径,再求出公共线与圆C1的交点,可得圆C1与圆C2相交的弦长.
解答:解:圆C1:x2-2x+y2=1,即 (x-1)2+y2=2,表示以C1(1,0)为圆心,半径等于
的圆.
圆C2:x2-4x+y2=0,即 (x-2)2+y2=4,表示以C2(2,0)为圆心半径等于2的圆.
把两个圆的方程相减,可得公共线所在的直线方程为 x=
,
再把x=
代入圆C1:x2-2x+y2=1,求得y=±
,故圆C1与圆C2相交的弦长为
,
故答案为
.
| 2 |
圆C2:x2-4x+y2=0,即 (x-2)2+y2=4,表示以C2(2,0)为圆心半径等于2的圆.
把两个圆的方程相减,可得公共线所在的直线方程为 x=
| 1 |
| 2 |
再把x=
| 1 |
| 2 |
| ||
| 2 |
| 7 |
故答案为
| 7 |
点评:本题主要考查两个圆的位置关系及其判定,求两个圆的公共线所在的直线方程的方法,属于中档题.

练习册系列答案
相关题目
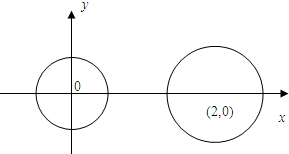 已知圆C1:x2+y2=1,圆C2:(x-4)2+y2=4
已知圆C1:x2+y2=1,圆C2:(x-4)2+y2=4