题目内容
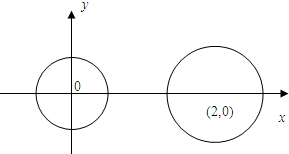 已知圆C1:x2+y2=1,圆C2:(x-4)2+y2=4
已知圆C1:x2+y2=1,圆C2:(x-4)2+y2=4(1)判断两圆位置关系;
(2)若直线l为过点P(3,0)且与圆C1相切的直线,求直线l的方程;
(3)在x轴上是否存在一定点Q(m,0),使得过Q点且与两圆都相交的直线被两圆所截得的弦长始终相等?若存在,求出Q点的坐标,若不存在,请说明理由.
分析:(1)由于两圆的圆心距|C1C2 |=4,大于两圆的半径之和,故两圆相离.
(2)由题意知,直线的斜率是存在的,由点斜式设出直线l的方程,由圆心C1 到直线l的距离等于半径,解方程求得
斜率k的值,即得直线l的方程.
(3)由题意知与两圆都相交的直线的斜率是存在的,由点斜式设出直线l的方程,设原点(0,0)和点(4,0)到该直线的距离分别为d1,d2,由题意可得
=
,化简可得(13-8m)k2=3恒成立,即13-8m=0,且3=0,矛盾.
从而得到结论.
(2)由题意知,直线的斜率是存在的,由点斜式设出直线l的方程,由圆心C1 到直线l的距离等于半径,解方程求得
斜率k的值,即得直线l的方程.
(3)由题意知与两圆都相交的直线的斜率是存在的,由点斜式设出直线l的方程,设原点(0,0)和点(4,0)到该直线的距离分别为d1,d2,由题意可得
| 1-d12 |
| 1-d22 |
从而得到结论.
解答:解:(1)由于圆C1:x2+y2=1,圆C2:(x-4)2+y2=4的圆心C1 (0,0),C2(4,0),半径分别为1和2.
两圆的圆心距|C1C2 |=4,大于两圆的半径之和,故两圆相离.
(2)由题意知,直线的斜率是存在的,设直线l的斜率为k,
则直线l的方程为 y-0=k(x-3),即kx-y-3k=0.
由圆心C1 到直线l的距离等于半径可得 1=
,∴k=±
.
故直线l的方程为
x-y-
=0,或
x+y-
=0.
(3)由题意知与两圆都相交的直线的斜率是存在的,
故可以设其方程为y-0=k(x-m),即kx-y-km=0.设原点(0,0)和点(4,0)到该直线的距离分别为d1,d2,由题意可得
=
,
即 d22-d12=3,∴(
)2-(
)2=3,
即16k2-8k2m=3+3k2,即 (13-8m)k2=3恒成立.
∴13-8m=0,且3=0,矛盾.
故不存在定点Q(m,0),使得过Q点且与两圆都相交的直线被两圆所截得的弦长始终相等.
两圆的圆心距|C1C2 |=4,大于两圆的半径之和,故两圆相离.
(2)由题意知,直线的斜率是存在的,设直线l的斜率为k,
则直线l的方程为 y-0=k(x-3),即kx-y-3k=0.
由圆心C1 到直线l的距离等于半径可得 1=
| |0-0-3k| | ||
|
| ||
| 4 |
故直线l的方程为
| ||
| 4 |
3
| ||
| 4 |
| ||
| 4 |
3
| ||
| 4 |
(3)由题意知与两圆都相交的直线的斜率是存在的,
故可以设其方程为y-0=k(x-m),即kx-y-km=0.设原点(0,0)和点(4,0)到该直线的距离分别为d1,d2,由题意可得
| 1-d12 |
| 1-d22 |
即 d22-d12=3,∴(
| |4k-km| | ||
|
| |km| | ||
|
即16k2-8k2m=3+3k2,即 (13-8m)k2=3恒成立.
∴13-8m=0,且3=0,矛盾.
故不存在定点Q(m,0),使得过Q点且与两圆都相交的直线被两圆所截得的弦长始终相等.
点评:本题主要考查两圆的位置关系的判定方法,直线和圆相交的性质,函数的恒成立问题,属于难题.

练习册系列答案
相关题目
 (2013•宁波模拟)如图,已知圆
(2013•宁波模拟)如图,已知圆