题目内容
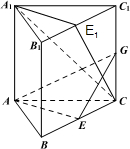
 (2011•天津模拟)如图,在三棱柱ABC-A1B1C1中,BB1⊥面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.
(2011•天津模拟)如图,在三棱柱ABC-A1B1C1中,BB1⊥面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.(1)求证:AE⊥B1C;
(2)求异面直线AE与A1C所成的角;
(3)若G为C1C中点,求二面角C-AG-E的正切值.
分析:(1)由BB1⊥面ABC及线面垂直的性质可得AE⊥BB1,由AC=AB,E是BC的中点,及等腰三角形三线合一,可得AE⊥BC,结合线面垂直的判定定理可证得AE⊥面BB1C1C,进而由线面垂直的性质得到AE⊥B1C;
(2)取B1C1的中点E1,连A1E1,E1C,根据异面直线夹角定义可得,∠E1A1C是异面直线A与A1C所成的角,设AC=AB=AA1=2,解三角形E1A1C可得答案.
(3)连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC,由直三棱锥的侧面与底面垂直,结合面面垂直的性质定理,可得EP⊥平面ACC1A1,进而由二面角的定义可得∠PQE是二面角C-AG-E的平面角.
(2)取B1C1的中点E1,连A1E1,E1C,根据异面直线夹角定义可得,∠E1A1C是异面直线A与A1C所成的角,设AC=AB=AA1=2,解三角形E1A1C可得答案.
(3)连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC,由直三棱锥的侧面与底面垂直,结合面面垂直的性质定理,可得EP⊥平面ACC1A1,进而由二面角的定义可得∠PQE是二面角C-AG-E的平面角.
解答:证明:(1)因为BB1⊥面ABC,AE?面ABC,所以AE⊥BB1-----------------(1分)
由AB=AC,E为BC的中点得到AE⊥BC-----------------(2分)
∵BC∩BB1=B∴AE⊥面BB1C1C----------------(3分)
∴AE⊥B1C-----------------(4分)
 解:(2)取B1C1的中点E1,连A1E1,E1C,
解:(2)取B1C1的中点E1,连A1E1,E1C,
则AE∥A1E1,
∴∠E1A1C是异面直线AE与A1C所成的角.----------------(6分)
设AC=AB=AA1=2,则由∠BAC=90°,
可得A1E1=AE=
,A1C=2
,E1C1=EC=
BC=
∴E1C=
=
∵在△E1A1C中,cos∠E1A1C=
=
------------------(8分)
所以异面直线AE与A1C所成的角为
.------------------(9分)
(3)连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC----(10分)
又∵平面ABC⊥平面ACC1A1
∴EP⊥平面ACC1A1-------------(11分)
而PQ⊥AG∴EQ⊥AG.
∴∠PQE是二面角C-AG-E的平面角.-------------(12分)
由EP=1,AP=1,PQ=
,得tan∠PQE=
=
所以二面角C-AG-E的平面角正切值是
-----------(13分)
由AB=AC,E为BC的中点得到AE⊥BC-----------------(2分)
∵BC∩BB1=B∴AE⊥面BB1C1C----------------(3分)
∴AE⊥B1C-----------------(4分)
 解:(2)取B1C1的中点E1,连A1E1,E1C,
解:(2)取B1C1的中点E1,连A1E1,E1C,则AE∥A1E1,
∴∠E1A1C是异面直线AE与A1C所成的角.----------------(6分)
设AC=AB=AA1=2,则由∠BAC=90°,
可得A1E1=AE=
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
∴E1C=
E1
|
| 6 |
∵在△E1A1C中,cos∠E1A1C=
| 2+8-6 | ||||
2•
|
| 1 |
| 2 |
所以异面直线AE与A1C所成的角为
| π |
| 3 |
(3)连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC----(10分)
又∵平面ABC⊥平面ACC1A1
∴EP⊥平面ACC1A1-------------(11分)
而PQ⊥AG∴EQ⊥AG.
∴∠PQE是二面角C-AG-E的平面角.-------------(12分)
由EP=1,AP=1,PQ=
| 1 | ||
|
| PE |
| PQ |
| 5 |
所以二面角C-AG-E的平面角正切值是
| 5 |
点评:本题是与二面角有关的立体几何综合题,主要考查了异面直线的夹角,线线垂直的判定,二面角等知识点,难度中档,熟练掌握线面垂直,线线垂直与面面垂直之间的转化及异面直线夹角及二面角的定义,是解答本题的关键.

练习册系列答案
相关题目
 (2011•天津模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )
(2011•天津模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则y=f(x)的图象可由函数g(x)=sinx的图象(纵坐标不变)( )