题目内容
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )一段图象如图所示
)一段图象如图所示
(1)分别求出A,ω,φ并确定函数f(x)的解析式
(2)求出f(x)的单调递增区间
(3)指出当f(x)取得最大值和最小值时x的集合.
解:(1)由函数的图象可知A=2,T=π,所以  ,ω=2,因为函数的图象经过(-
,ω=2,因为函数的图象经过(- .0),
.0),
所以0=2sin(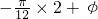 ),又
),又  ,所以φ=
,所以φ= ;
;
所以函数的解析式为:y=2sin(2x+ )
)
(2)∵正弦函数的单调递增区间是[2k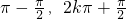 ]
]
∴2x+ ∈[2k
∈[2k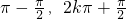 ]
]
∴函数的单调递增区间是[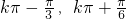 ](k∈Z)
](k∈Z)
(3)∵当正弦曲线取得最大值时,对应的2x+ =2k
=2k
当正弦曲线取得最小值时,对应的2x+ =2k
=2k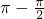
∴当f(x)取得最小值时x的集合为{x|x=kπ- ,k∈Z}
,k∈Z}
当f(x)取得最大值时x的集合为{x|x=kπ+ ,k∈Z}.
,k∈Z}.
分析:(1)通过函数的图象求出A,周期T,利用周期公式求出ω,图象经过(- ,0)以及φ的范围,求出φ的值,得到函数的解析式.
,0)以及φ的范围,求出φ的值,得到函数的解析式.
(2)写出正弦曲线的单调递增区间,使得函数的角对应的函数式在这个区间,求出自变量x的取值范围.
(3)当正弦曲线取得最大值时,对应的2x+ =2k
=2k ,当正弦曲线取得最小值时,对应的2x+
,当正弦曲线取得最小值时,对应的2x+ =2k
=2k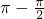 ,通过解不等式做出函数对应的自变量的取值.
,通过解不等式做出函数对应的自变量的取值.
点评:题是基础题,考查三角函数的图象求函数的解析式的方法,考查学生的视图能力,计算能力,是一种常考题型.
 ,ω=2,因为函数的图象经过(-
,ω=2,因为函数的图象经过(- .0),
.0),所以0=2sin(
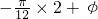 ),又
),又  ,所以φ=
,所以φ= ;
;所以函数的解析式为:y=2sin(2x+
 )
) (2)∵正弦函数的单调递增区间是[2k
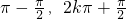 ]
]∴2x+
 ∈[2k
∈[2k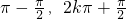 ]
]∴函数的单调递增区间是[
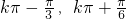 ](k∈Z)
](k∈Z) (3)∵当正弦曲线取得最大值时,对应的2x+
 =2k
=2k
当正弦曲线取得最小值时,对应的2x+
 =2k
=2k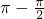
∴当f(x)取得最小值时x的集合为{x|x=kπ-
 ,k∈Z}
,k∈Z}当f(x)取得最大值时x的集合为{x|x=kπ+
 ,k∈Z}.
,k∈Z}.分析:(1)通过函数的图象求出A,周期T,利用周期公式求出ω,图象经过(-
 ,0)以及φ的范围,求出φ的值,得到函数的解析式.
,0)以及φ的范围,求出φ的值,得到函数的解析式.(2)写出正弦曲线的单调递增区间,使得函数的角对应的函数式在这个区间,求出自变量x的取值范围.
(3)当正弦曲线取得最大值时,对应的2x+
 =2k
=2k ,当正弦曲线取得最小值时,对应的2x+
,当正弦曲线取得最小值时,对应的2x+ =2k
=2k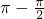 ,通过解不等式做出函数对应的自变量的取值.
,通过解不等式做出函数对应的自变量的取值.点评:题是基础题,考查三角函数的图象求函数的解析式的方法,考查学生的视图能力,计算能力,是一种常考题型.

练习册系列答案
相关题目
 如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为
如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<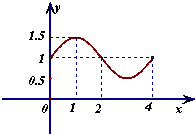 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2008)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2008)的值分别为( )